题目内容
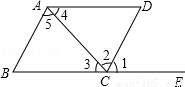
1. 用长为8m的铝合金制成如图所示形状的矩形窗框,使窗户的透光面积最大,那么这个窗户的最大透光面积是$\frac{8}{3}$m2(铝合金条遮光部分忽略不计).
用长为8m的铝合金制成如图所示形状的矩形窗框,使窗户的透光面积最大,那么这个窗户的最大透光面积是$\frac{8}{3}$m2(铝合金条遮光部分忽略不计).
分析 设窗的高度为xm,宽为$\frac{8-2x}{3}$m,则根据矩形面积公式列出二次函数求函数值的最大值即可.
解答 解:设窗的高度为xm,宽为($\frac{8-2x}{3}$)m,
故S=$\frac{x(8-2x)}{3}$.
∴$\frac{3S}{2}$=x(4-x),
即S=-$\frac{2}{3}$(x-2)2+$\frac{8}{3}$.
∴当x=2m时,S最大值为$\frac{8}{3}$m2.
点评 本题主要考查了二次函数的应用,根据矩形面积公式列出函数表达式是解决问题的关键.

练习册系列答案
相关题目
17.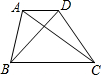 如图,在梯形ABCD中AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则AD+BC=( )
如图,在梯形ABCD中AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则AD+BC=( )
 如图,在梯形ABCD中AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则AD+BC=( )
如图,在梯形ABCD中AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则AD+BC=( )| A. | 20 | B. | 21 | C. | 15 | D. | 24 |
9.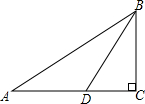 如图,在Rt△ABC中,∠C=90°,BD是角平分线,若CD=m,AB=n,则△ABD的面积是( )
如图,在Rt△ABC中,∠C=90°,BD是角平分线,若CD=m,AB=n,则△ABD的面积是( )
 如图,在Rt△ABC中,∠C=90°,BD是角平分线,若CD=m,AB=n,则△ABD的面积是( )
如图,在Rt△ABC中,∠C=90°,BD是角平分线,若CD=m,AB=n,则△ABD的面积是( )| A. | mn | B. | $\frac{1}{2}mn$ | C. | 2mn | D. | $\frac{1}{3}mn$ |
10.已知对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,则它的对称轴为( )
| A. | x=1 | B. | x=2 | C. | x=3 | D. | x=2.5 |
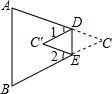 如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=40°,则∠2的度数为40°.
如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=40°,则∠2的度数为40°.