题目内容
已知方程x2-(2k-1)x+k-4=0,实数k分别取何值时:
(1)两实根异号,且正根的绝对值较大;
(2)一个根大于3,另一个根小于3.
(1)两实根异号,且正根的绝对值较大;
(2)一个根大于3,另一个根小于3.
考点:抛物线与x轴的交点
专题:
分析:(1)根据一元二次方程有两个不相等的实根,则判别式△>0,并且正根的绝对值较大,则两根的和大于0,且两根的积小于0,根据一元二次方程的根与系数的关系即可得到关于k的不等式组,即可求得k的范围;
(2)设方程的两个根分别是x1、x2,根据题意,得(x1-3)(x2-3)<0,根据一元二次方程根与系数的关系即可求得k的取值范围,再根据△>0确定k的范围.
(2)设方程的两个根分别是x1、x2,根据题意,得(x1-3)(x2-3)<0,根据一元二次方程根与系数的关系即可求得k的取值范围,再根据△>0确定k的范围.
解答:解:方程x2-(2k-1)x+k-4=0的根的判别式为:△=[-(2k-1)]2-4(k-4),
整理,得4(k-1)2+13>0.
则k取任意实数.
(1)设方程的两个根为x1、x2,则:
∵两实根异号,且正根的绝对值较大,
∴x1+x2=2k-3>0,且x1x2=2k-4<0,
解得:
<k<2,
所以k的取值范围是
<k<2;
(2)设方程的两个根为x1、x2,则:
x1+x2=2k-3>0,且x1x2=2k-4<0
∵一个根大于3,另一个根小于3
∴(x1-3)(x2-3)<0
x1•x2-3(x1+x2)+9=2k-4-6k+9+9<0,即:-4k+14<0.
解得 k>
故k的取值范围为:k>
.
整理,得4(k-1)2+13>0.
则k取任意实数.
(1)设方程的两个根为x1、x2,则:
∵两实根异号,且正根的绝对值较大,
∴x1+x2=2k-3>0,且x1x2=2k-4<0,
解得:
| 3 |
| 2 |
所以k的取值范围是
| 3 |
| 2 |
(2)设方程的两个根为x1、x2,则:
x1+x2=2k-3>0,且x1x2=2k-4<0
∵一个根大于3,另一个根小于3
∴(x1-3)(x2-3)<0
x1•x2-3(x1+x2)+9=2k-4-6k+9+9<0,即:-4k+14<0.
解得 k>
| 7 |
| 2 |
故k的取值范围为:k>
| 7 |
| 2 |
点评:此题主要是一元二次方程根的判别式及根与系数的关系的运用,在已知方程的一根x1比常数a大,一根x2比常数a小的时候,可列(x1-a)(x2-a)<0的不等式分析求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,四边形ABCD的两条对角线相交于点P,∠ADB=∠BCA,DC=AP=6,DP=3,则AB=( )
如图,四边形ABCD的两条对角线相交于点P,∠ADB=∠BCA,DC=AP=6,DP=3,则AB=( )| A、15 | B、12 | C、9 | D、6 |
如图,图中数轴的单位长度为1.如果点B,C表示的数的绝对值相等,那么点A与点D表示的数分别是( )

| A、-2,2 | B、-4,1 |
| C、-5,1 | D、-6,2 |
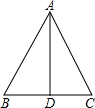 如图,在△ABC中,AB=AC,∠BAD=∠CAD,则下列结论:
如图,在△ABC中,AB=AC,∠BAD=∠CAD,则下列结论: 如图,M、N分别为AB、BC的中点,AC=8cm,求MN.
如图,M、N分别为AB、BC的中点,AC=8cm,求MN. 已知抛物线y=x2-4x+3.
已知抛物线y=x2-4x+3.