题目内容
12.某高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的$\frac{2}{3}$;若由甲队先做20天,剩下的工程再由甲、乙两队合作60天完成.(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.6万元,乙队每天的施工费用为5.4万元.工程预算的施工费用为1000万元.若在甲、乙工程队工作效率不变的情况下使施工时间最短,问拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?
分析 (1)首先表示出甲、乙两队需要的天数,进而利用由甲队先做20天,剩下的工程再由甲、乙两队合作60天完成得出等式求出答案;
(2)首先求出两队合作需要的天数,进而求出答案.
解答 解:(1)设乙队单独完成这项工程需要x天,则甲队单独完成这项工程需要$\frac{2}{3}$x天.
根据题意,得$\frac{20}{\frac{2x}{3}}$+60×($\frac{1}{\frac{2x}{3}}$+$\frac{1}{x}$)=1,
解得:x=180.
经检验,x=180是原方程的根.
∴$\frac{2x}{3}$=$\frac{2}{3}$×180=120,
答:甲、乙两队单独完成这项工程分别需120天和180天;
(2)设甲、乙两队合作完成这项工程需要y天,
则有y($\frac{1}{120}$+$\frac{1}{180}$)=1,
解得 y=72.
需要施工费用:72×(8.6+5.4)=1008(万元).
∵1008>1000.
∴工程预算的施工费用不够用,需追加预算8万元.
点评 此题主要考查了分式方程的应用以及一元一次方程的应用,正确得出等量关系是解题关键.

练习册系列答案
相关题目
20.为了解某社区居民的用电情况,随机对该社区15户居民进行调查,下表是这15户居民2015年4月份用电量的调查结果:
那么关于这15户居民月用电量(单位:度),下列说法错误的是( )
| 居民(户) | 5 | 3 | 3 | 4 |
| 月用电量(度/户) | 30 | 42 | 50 | 51 |
| A. | 平均数是43.25 | B. | 众数是30 | C. | 方差是82.4 | D. | 中位数是42 |
17.下列图形中,周长最长的是( )
| A. |  | B. |  | C. |  | D. |  |
6.(x2+mx+1)(x-3)的积中x的二次项系数为零,则m的值是( )
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
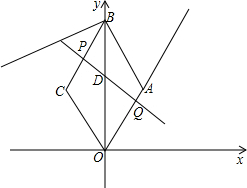 已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是(0,8$\sqrt{3}$),点P从点C开始以每秒1个单位长度的速度沿线段CB向点B移动,同时,点Q从点O开始以每秒3个单位长度的速度沿射线OA方向移动,点P运动到点B时,两点停止运动.直线PQ交OB于点D,运动时间为t秒.
已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是(0,8$\sqrt{3}$),点P从点C开始以每秒1个单位长度的速度沿线段CB向点B移动,同时,点Q从点O开始以每秒3个单位长度的速度沿射线OA方向移动,点P运动到点B时,两点停止运动.直线PQ交OB于点D,运动时间为t秒.