题目内容
9.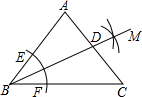 在△ABC中,AB=AC,∠A=80°,进行如下操作:
在△ABC中,AB=AC,∠A=80°,进行如下操作:①以点B为圆心,以小于AB长为半径作弧,分别交BA、BC于点E、F;
②分别以E、F为圆心,以大于$\frac{1}{2}$EF长为半径作弧,两弧交于点M;
③作射线BM交AC于点D,
则∠BDC的度数为( )
| A. | 100° | B. | 65° | C. | 75° | D. | 105° |
分析 利用等腰三角形的性质结合三角形内角和定理得出∠ABC=∠C=50°,再利用角平分线的性质与作法得出即可.
解答 解:∵AB=AC,∠A=80°,
∴∠ABC=∠C=50°,
由题意可得:BD平分∠ABC,
则∠ABD=∠CBD=25°,
∴∠BDC的度数为:∠A+∠ABD=105°.
故选:D.
点评 此题主要考查了基本作图以及等腰三角形的性质,得出BD平分∠ABC是解题关键.

练习册系列答案
相关题目
20.若二元一次方程式组$\left\{\begin{array}{l}{5x-y=5}\\{y=\frac{1}{5}x}\end{array}\right.$的解为x=a,y=b,则a+b等于( )
| A. | $\frac{5}{4}$ | B. | $\frac{75}{13}$ | C. | $\frac{31}{25}$ | D. | $\frac{29}{25}$ |
17.“五一”节老同学聚会,每两个人都握一次手,所有人共握手28次,则参加聚会的人数是( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
14. 某校学校兴趣小组对“是否赞成中学生上学带手机”问题进行了社会调查,小明将随机调查得到的数据列出下列频数分布表和频数分别直方图(不完整).
某校学校兴趣小组对“是否赞成中学生上学带手机”问题进行了社会调查,小明将随机调查得到的数据列出下列频数分布表和频数分别直方图(不完整).
频数分布表:
(1)请求出共调查了多少人?
(2)把频数分布表和频数分布直方图补充完整;
(3)小颖要将调查数据绘制成扇形统计图,则扇形图中“赞成”的圆心角是多少度?
 某校学校兴趣小组对“是否赞成中学生上学带手机”问题进行了社会调查,小明将随机调查得到的数据列出下列频数分布表和频数分别直方图(不完整).
某校学校兴趣小组对“是否赞成中学生上学带手机”问题进行了社会调查,小明将随机调查得到的数据列出下列频数分布表和频数分别直方图(不完整).频数分布表:
| 看法 | 频数 | 频率 |
| 赞成 | 3 | 0.05 |
| 无所谓 | 12 | 0.20 |
| 反对 | 45 | 0.75 |
(2)把频数分布表和频数分布直方图补充完整;
(3)小颖要将调查数据绘制成扇形统计图,则扇形图中“赞成”的圆心角是多少度?
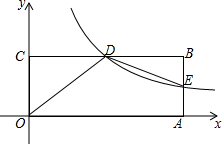 如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=$\frac{4}{3}$.
如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=$\frac{4}{3}$.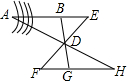 如图所示,要测量AB的长,因为无法过河接近点A,可以作AB外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到G,使DG=BD,延长ED到F,使DF=ED,连接FG,并延长FG到H,使H、D、A在一直线上,则HG=AB,试说明这种测量方法的原理.
如图所示,要测量AB的长,因为无法过河接近点A,可以作AB外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到G,使DG=BD,延长ED到F,使DF=ED,连接FG,并延长FG到H,使H、D、A在一直线上,则HG=AB,试说明这种测量方法的原理.