题目内容
18.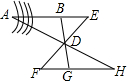 如图所示,要测量AB的长,因为无法过河接近点A,可以作AB外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到G,使DG=BD,延长ED到F,使DF=ED,连接FG,并延长FG到H,使H、D、A在一直线上,则HG=AB,试说明这种测量方法的原理.
如图所示,要测量AB的长,因为无法过河接近点A,可以作AB外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到G,使DG=BD,延长ED到F,使DF=ED,连接FG,并延长FG到H,使H、D、A在一直线上,则HG=AB,试说明这种测量方法的原理.
分析 利用全等三角形的判定与性质得出△BED≌△GFD(SAS),以及△ABD≌△HGD(ASA),进而得出答案.
解答 解:∵在△BED和△GFD中
$\left\{\begin{array}{l}{BD=DG}\\{∠BDE=∠GDF}\\{DE=FD}\end{array}\right.$,
∴△BED≌△GFD(SAS),
∴∠E=∠F,∠EBD=∠FGD,
∴∠ABD=∠HGD,
在△ABD和△HGD中
∵$\left\{\begin{array}{l}{∠ABD=∠HGD}\\{BD=DG}\\{∠BDA=∠GDH}\end{array}\right.$,
∴△ABD≌△HGD(ASA),
∴HG=AB,
即利用全等三角形的性质对应边相等.
点评 此题主要考查了全等三角形的判定与性质,得出△ABD≌△HGD是解题关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
8.已知x=-3是关于x的方程2x-a=1的解,则a的值是( )
| A. | -5 | B. | 5 | C. | -7 | D. | 2 |
9.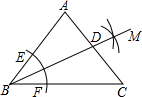 在△ABC中,AB=AC,∠A=80°,进行如下操作:
在△ABC中,AB=AC,∠A=80°,进行如下操作:
①以点B为圆心,以小于AB长为半径作弧,分别交BA、BC于点E、F;
②分别以E、F为圆心,以大于$\frac{1}{2}$EF长为半径作弧,两弧交于点M;
③作射线BM交AC于点D,
则∠BDC的度数为( )
 在△ABC中,AB=AC,∠A=80°,进行如下操作:
在△ABC中,AB=AC,∠A=80°,进行如下操作:①以点B为圆心,以小于AB长为半径作弧,分别交BA、BC于点E、F;
②分别以E、F为圆心,以大于$\frac{1}{2}$EF长为半径作弧,两弧交于点M;
③作射线BM交AC于点D,
则∠BDC的度数为( )
| A. | 100° | B. | 65° | C. | 75° | D. | 105° |
6.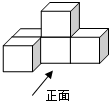 如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法错误的是( )
如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法错误的是( )
 如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法错误的是( )
如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法错误的是( )| A. | 主视图的面积为4 | B. | 左视图的面积为3 | ||
| C. | 俯视图的面积为4 | D. | 搭成的几何体的表面积是20 |
 如图,已知?ABCD的周长为8cm,∠B=45°,AB=AD,AE⊥BC于点E.求AE的长度及?ABCD的面积.
如图,已知?ABCD的周长为8cm,∠B=45°,AB=AD,AE⊥BC于点E.求AE的长度及?ABCD的面积. 如图,在△ABC中,AB=AC=10,BC=12,点D是AB的中点,点E是AC上一点,且AD=DE,连接BE,则BE的长为9.6.
如图,在△ABC中,AB=AC=10,BC=12,点D是AB的中点,点E是AC上一点,且AD=DE,连接BE,则BE的长为9.6.