题目内容
7. 如图,已知点A,B是数轴上两点(点B在点A右边),O为原点,点A对应着数8,AB=4.解答下列问题:
如图,已知点A,B是数轴上两点(点B在点A右边),O为原点,点A对应着数8,AB=4.解答下列问题:(1)点B对应的数是12;
(2)C,D两点同时从点A,原点O出发分别以1cm/s和2cm/s的速度沿数轴正方向运动,设运动时间为ts.
①当t=2时,BC=$\frac{1}{2}$AD(填上数量关系).
②当运动ts后,点C对应的数是8+t;点D对应的数是2t.(分别用含t的代数式表示).
③若数轴上点A,B所代表的数分别表示a,b(b>a),则A,B两点之间的距离可表示为AB=b-a(较大数-较小数),当t>4时,且CD=AB,求t的值.
④取线段CD的中点M,当BM=$\frac{1}{4}$OA时,求t的值.
分析 (1)结合数轴由点A对应着数8,AB=4,且点B在点A右边可得;
(2)①求出t=2时,BC、AD的长即可得;
②根据C、D两点的运动速度及时间t可得其运动的路程,结合数轴可得答案;
③分点D在点C的左侧和右侧,根据两点间的距离公式,结合CD=AB列出方程求解可得;
④由②知CD的中点M所表示的数为$\frac{2t+8+t}{2}$=$\frac{3t+8}{2}$,再根据两点间的距离公式,结合BM=$\frac{1}{4}$OA列出方程求解可得.
解答 解:(1)∵点A对应着数8,AB=4,且点B在点A右边,
∴点B表示的数为12,
故答案为:12;
(2)①当t=2时,BC=12-8-2=2,AD=8-2×2=4,
∴BC=$\frac{1}{2}$AD,
故答案为:$\frac{1}{2}$;
②运动ts后,点C对应的数为8+t,点D对应的数为2t,
故答案为:8+t,2t;
③当点D在点C的左侧时,由CD=AB可得8+t-2t=4,解得:t=4(舍);
当点D在点C的右侧时,由CD=AB可得2t-(8+t)=4,解得:t=12;
④当点D在点C的左侧时,由BM=$\frac{1}{4}$OA可得12-$\frac{3t+8}{2}$=$\frac{1}{4}$×8,解得:t=4;
当点D在点C的右侧时,由BM=$\frac{1}{4}$OA可得$\frac{3t+8}{2}$-12=$\frac{1}{4}$×8,解得:t=$\frac{20}{3}$.
点评 本题主要考查数轴和一元一次方程的应用,熟练掌握两点间的距离公式和中点公式是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
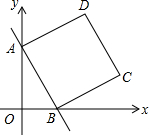 如图,一次函数y=-$\frac{4}{3}$x+4的图象与x轴和y轴分别交于点B和点A,以AB为边在第一象限内作正方形ABCD.
如图,一次函数y=-$\frac{4}{3}$x+4的图象与x轴和y轴分别交于点B和点A,以AB为边在第一象限内作正方形ABCD. 如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,则∠DFE=100°,EC=2.
如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,则∠DFE=100°,EC=2.