题目内容
18.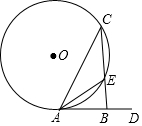 如图,在⊙O中,AC是弦,AD是切线,CB⊥AD于B,CB与⊙O相交于点E,连接AE,若AE平分∠BAC,BE=1,则CE=2.
如图,在⊙O中,AC是弦,AD是切线,CB⊥AD于B,CB与⊙O相交于点E,连接AE,若AE平分∠BAC,BE=1,则CE=2.
分析 根据弦切角的性质得∠C=∠BAE,再由已知条件求得∠C=∠BAE=∠CAE,从而求出∠C=∠BAE=∠CAE=30°,最后根据
含30°直角三角形的性质即可求出结论.
解答 解:∵AD是切线,
∴∠C=∠BAE,
∵∠BAE=∠CAE,
∴∠C=∠BAE=∠CAE,
∵CB⊥AD,
∴∠C+∠BAE+∠CAE=90°,
∴∠C=∠BAE=∠CAE=30°,
∴CE=AE=2BE=2,
故答案为2.
点评 本题主要考查了弦切角定理,角平分线,垂直定义,能根据弦切角的性质证得∠C=∠BAE是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
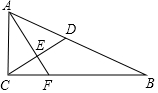 如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在AB上,AD=AC,AF⊥CD交CD于点E,交BC于点F,则CF=$\frac{10}{3}$.
如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在AB上,AD=AC,AF⊥CD交CD于点E,交BC于点F,则CF=$\frac{10}{3}$. 如图,△ABC中,点D为BC中点,点E为AD中点,点F为CE中点,若S△ABC=10cm2,则S△BEF=2.5cm2.
如图,△ABC中,点D为BC中点,点E为AD中点,点F为CE中点,若S△ABC=10cm2,则S△BEF=2.5cm2.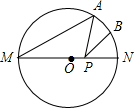 如图,MN是⊙O的直径,MN=10,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为5$\sqrt{2}$.
如图,MN是⊙O的直径,MN=10,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为5$\sqrt{2}$. 如图,直线y1=kx+b与双曲线y2=$\frac{m}{x}$交于A,B两点,它们的横坐标分别为1和5.
如图,直线y1=kx+b与双曲线y2=$\frac{m}{x}$交于A,B两点,它们的横坐标分别为1和5.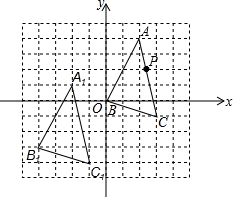 在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为(1.6,1).
在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为(1.6,1).