题目内容
13．已知一次函数y=-mx+4和y=3x-n的图象交于点P（3，1），则关于x的方程组$\left\{\begin{array}{l}{mx+y=4}\\{3x-y=n}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$．分析 根据方程组的解即为函数图象的交点坐标解答．
解答 解：∵一次函数y=-mx+4和y=3x-n的图象交于点P（3，1），
∴方程组 $\left\{\begin{array}{l}{mx+y=4}\\{3x-y=n}\end{array}\right.$的解是 $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$；
故答案为：$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$
点评 本题主要考查了函数解析式与图象的关系，满足解析式的点就在函数的图象上，在函数的图象上的点，就一定满足函数解析式．函数图象交点坐标为两函数解析式组成的方程组的解．
练习册系列答案
相关题目
4．
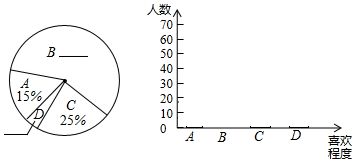某校为了进一步改变本校七年级数学教学，提高学生学习数学的兴趣，校教务处在七年级所有班级中，每班随机抽取了6名学生，并对他们的数学学习情况进行了问卷调查，我们从所调查的题目中，特别把学生对数学学习喜欢程度的回答（喜欢程度分为：“A．非常喜欢”、“B．比较喜欢”、“C．不太喜欢”、“D．很不喜欢”，针对这个题目，问卷时要求每位被调查的学生必须从中选一项且只能选一项）结果进行了统计，现将统计结果绘制成如下三幅不完整的统计图表．
请你根据以上提供的信息，解答下列问题：
（1）补全上面的频数分布表和扇形统计图；
（2）根据补全的频数分布表画出频数分布直方图；
（3）若该校七年级共有600名学生，请你估算该年级学生中对数学学习“不太喜欢”的有多少人？
某校为了进一步改变本校七年级数学教学，提高学生学习数学的兴趣，校教务处在七年级所有班级中，每班随机抽取了6名学生，并对他们的数学学习情况进行了问卷调查，我们从所调查的题目中，特别把学生对数学学习喜欢程度的回答（喜欢程度分为：“A．非常喜欢”、“B．比较喜欢”、“C．不太喜欢”、“D．很不喜欢”，针对这个题目，问卷时要求每位被调查的学生必须从中选一项且只能选一项）结果进行了统计，现将统计结果绘制成如下三幅不完整的统计图表． | 喜欢程度 | 频数 |
| A | 18 |
| B | 66 |
| C | 30 |
| D | 6 |
（1）补全上面的频数分布表和扇形统计图；
（2）根据补全的频数分布表画出频数分布直方图；
（3）若该校七年级共有600名学生，请你估算该年级学生中对数学学习“不太喜欢”的有多少人？
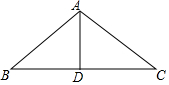如图，在△ABC中，AB=5cm，BC=8cm，BC边上的中线AD=3cm，求∠ADC的度数．
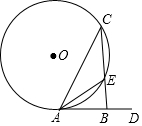如图，在⊙O中，AC是弦，AD是切线，CB⊥AD于B，CB与⊙O相交于点E，连接AE，若AE平分∠BAC，BE=1，则CE=2．
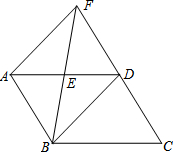如图，?ABCD中，E为AD的中点，直线BE、CD相交于点F．连接AF、BD．