题目内容
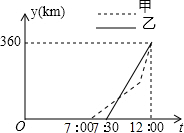 甲、乙两车从A地前往B地,甲车行至AB的中点C处后,以原来速度的1.5倍继续行驶,在整个行程中,汽车离开A地的距离y与时刻t的对应关系如图所示,求:
甲、乙两车从A地前往B地,甲车行至AB的中点C处后,以原来速度的1.5倍继续行驶,在整个行程中,汽车离开A地的距离y与时刻t的对应关系如图所示,求:(1)甲车何时到达C地;
(2)甲车离开A地的距离y与时刻t的函数解析式;
(3)乙车出发后何时与甲车相距20km.
考点:一次函数的应用
专题:
分析:(1)设甲车t时到达C地,根据甲车行至AB的中点C处后,以原来速度的1.5倍继续行驶,结合图象列出方程1.5×
=
,解方程即可;
(2)分两种情况:①7≤t≤10;②10<t≤12;利用待定系数法即可求出;
(3)先利用待定系数法求出乙车离开A地的距离y与时刻t的函数解析式,再分甲车在乙车的前面与乙车在甲车的前面两种情况列出方程,解方程即可.
| 180 |
| t-7 |
| 180 |
| 12-t |
(2)分两种情况:①7≤t≤10;②10<t≤12;利用待定系数法即可求出;
(3)先利用待定系数法求出乙车离开A地的距离y与时刻t的函数解析式,再分甲车在乙车的前面与乙车在甲车的前面两种情况列出方程,解方程即可.
解答:解:(1)设甲车t时到达C地,由题意得,
1.5×
=
,
解得t=10,
经检验,t=10是原方程的根,
故甲车10:00到达C地;
(2)当7≤t≤10时,由图象过点(7,0)和(10,180),可得y=60t-420;
当10<t≤12时,由图象过点(10,180)和(12,360),可得y=90t-720;
故甲车离开A地的距离y与时刻t的函数解析式为:
y甲=
;
(3)当7.5≤t≤12时,由图象过点(7.5,0)和(12,360),可得y=80t-600,
所以乙车离开A地的距离y与时刻t的函数解析式为:y乙=80t-600(7.5≤t≤12).
若y甲≥y乙,则(60t-420)-(80t-600)=20,解得t=8;
若y甲<y乙,则(80t-600)-(60t-420)=20,解得t=10;
或(80t-600)-(90t-720)=20,解得t=10.
故乙车出发后共有两次与甲车相距20km,第一次在8:00,第二次在10:00.
1.5×
| 180 |
| t-7 |
| 180 |
| 12-t |
解得t=10,
经检验,t=10是原方程的根,
故甲车10:00到达C地;
(2)当7≤t≤10时,由图象过点(7,0)和(10,180),可得y=60t-420;
当10<t≤12时,由图象过点(10,180)和(12,360),可得y=90t-720;
故甲车离开A地的距离y与时刻t的函数解析式为:
y甲=
|
(3)当7.5≤t≤12时,由图象过点(7.5,0)和(12,360),可得y=80t-600,
所以乙车离开A地的距离y与时刻t的函数解析式为:y乙=80t-600(7.5≤t≤12).
若y甲≥y乙,则(60t-420)-(80t-600)=20,解得t=8;
若y甲<y乙,则(80t-600)-(60t-420)=20,解得t=10;
或(80t-600)-(90t-720)=20,解得t=10.
故乙车出发后共有两次与甲车相距20km,第一次在8:00,第二次在10:00.
点评:本题考查了一次函数的应用,分式方程与一元一次方程的应用,一次函数解析式的确定,难度适中.从函数图象中获取有用信息是解题的关键.

练习册系列答案
相关题目
 如图,在数轴上表示
如图,在数轴上表示| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、2
| ||||
D、2
|
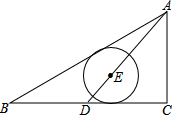 如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为( )
如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为( )A、
| ||||
B、
| ||||
C、
| ||||
D、1≤R≤
|
 已知AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连接OC,若∠ABO=32°,则∠AOC=
已知AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连接OC,若∠ABO=32°,则∠AOC=