题目内容
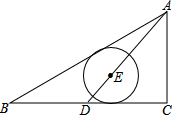 如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为( )
如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为( )A、
| ||||
B、
| ||||
C、
| ||||
D、1≤R≤
|
考点:切线的性质
专题:计算题
分析:当点E在AD上,AD为△ABC的中线,如图1,作EH⊥BC于H,EF⊥AB于F,根据切线的性质得EH=EF=R,在Rt△ABC中利用勾股定理计算出BC=4,在Rt△ADC中,根据勾股定理计算出AD=
,然后证明△DEH∽△DAC,利用相似比得到DE=
R,DH=
R,则AE=AD-DE=
-
R,BH=BD+DH=2+
R,则根据切线长定理得BF=BH=2+
R,所以AF=AB-BF=3-
R,再在Rt△AEF中根据勾股定理得到R2+(3-
R)2=(
-
R)2,解得R=
;
当点D运动到点C的位置,如图2,作EF⊥AB于F,利用切线的性质得EC=EF=R,则AE=AC-EC=3-R,再证明Rt△AFE∽Rt△ACB,利用相似比可计算出R=
,
由于D为BC的中点时,⊙E的半径最小,D点与C点重合时,⊙E的半径最大,所以则⊙E的半径R的取值范围为
≤R≤
.
| 13 |
| ||
| 3 |
| 2 |
| 3 |
| 13 |
| ||
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 13 |
| ||
| 3 |
| 6 |
| 7 |
当点D运动到点C的位置,如图2,作EF⊥AB于F,利用切线的性质得EC=EF=R,则AE=AC-EC=3-R,再证明Rt△AFE∽Rt△ACB,利用相似比可计算出R=
| 4 |
| 3 |
由于D为BC的中点时,⊙E的半径最小,D点与C点重合时,⊙E的半径最大,所以则⊙E的半径R的取值范围为
| 6 |
| 7 |
| 4 |
| 3 |
解答:解:当点E在AD上,AD为△ABC的中线,如图1,作EH⊥BC于H,EF⊥AB于F,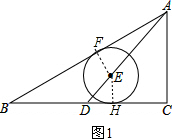
∵以E为圆心的⊙E分别与AB、BC相切,
∴EH=EF=R,
在Rt△ABC中,∵∠C=90°,AB=5,AC=3,
∴BC=
=4,
∵点D为BC的中点,
∴BD=CD=2,
在Rt△ADC中,AD=
=
,
∵EH∥AC,
∴△DEH∽△DAC,
∴
=
=
,即
=
=
,
∴DE=
R,DH=
R,
∴AE=AD-DE=
-
R,BH=BD+DH=2+
R,
∵以E为圆心的⊙E分别与AB、BC相切,
∴BF=BH=2+
R
∴AF=AB-BF=3-
R,
在Rt△AEF中,∵EF2+AF2=AE2,
∴R2+(3-
R)2=(
-
R)2,解得R=
;
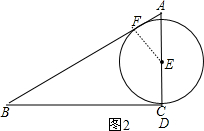 当点D运动到点C的位置,如图2,作EF⊥AB于F,
当点D运动到点C的位置,如图2,作EF⊥AB于F,
∵以E为圆心的⊙E分别与AB、BC相切,
∴EC=EF=R,
∴AE=AC-EC=3-R,
∵∠FAE=∠CAB,
∴Rt△AFE∽Rt△ACB,
∴
=
,即
=
,解得R=
,
∴当D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为
≤R≤
.
故选B.

∵以E为圆心的⊙E分别与AB、BC相切,
∴EH=EF=R,
在Rt△ABC中,∵∠C=90°,AB=5,AC=3,
∴BC=
| AB2-AC2 |
∵点D为BC的中点,
∴BD=CD=2,
在Rt△ADC中,AD=
| AC2+CD2 |
| 13 |
∵EH∥AC,
∴△DEH∽△DAC,
∴
| DE |
| DA |
| EH |
| AC |
| DH |
| DC |
| DE | ||
|
| R |
| 3 |
| DH |
| 2 |
∴DE=
| ||
| 3 |
| 2 |
| 3 |
∴AE=AD-DE=
| 13 |
| ||
| 3 |
| 2 |
| 3 |
∵以E为圆心的⊙E分别与AB、BC相切,
∴BF=BH=2+
| 2 |
| 3 |
∴AF=AB-BF=3-
| 2 |
| 3 |
在Rt△AEF中,∵EF2+AF2=AE2,
∴R2+(3-
| 2 |
| 3 |
| 13 |
| ||
| 3 |
| 6 |
| 7 |
 当点D运动到点C的位置,如图2,作EF⊥AB于F,
当点D运动到点C的位置,如图2,作EF⊥AB于F,∵以E为圆心的⊙E分别与AB、BC相切,
∴EC=EF=R,
∴AE=AC-EC=3-R,
∵∠FAE=∠CAB,
∴Rt△AFE∽Rt△ACB,
∴
| EF |
| BC |
| AE |
| AB |
| R |
| 4 |
| 3-R |
| 5 |
| 4 |
| 3 |
∴当D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为
| 6 |
| 7 |
| 4 |
| 3 |
故选B.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点;经过切点且垂直于切线的直线必经过圆心.也考查了勾股定理和相似三角形的判定与性质.

练习册系列答案
相关题目
下列实数:3.14,π,0.121121112中无理数的个数为( )
| A、1 | B、2 | C、3 | D、4 |
 若a,b,c的位置如右图,则a-(b-c)的值是( )
若a,b,c的位置如右图,则a-(b-c)的值是( )| A、负数 | B、正数 |
| C、整数 | D、不能确定 |
下列各组的两个数中,运算后结果相等的是( )
| A、-32与(-3)2 | ||||
| B、53与35 | ||||
| C、-73与(-7)3 | ||||
D、(-
|
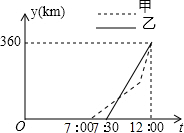 甲、乙两车从A地前往B地,甲车行至AB的中点C处后,以原来速度的1.5倍继续行驶,在整个行程中,汽车离开A地的距离y与时刻t的对应关系如图所示,求:
甲、乙两车从A地前往B地,甲车行至AB的中点C处后,以原来速度的1.5倍继续行驶,在整个行程中,汽车离开A地的距离y与时刻t的对应关系如图所示,求: