题目内容
 已知AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连接OC,若∠ABO=32°,则∠AOC=
已知AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连接OC,若∠ABO=32°,则∠AOC=考点:等腰三角形的判定与性质
专题:
分析:根据角平分线的性质,可得∠OBD与∠ABO的关系,根据线段垂直平分线的性质,可得△OBC的形状,可得∠C与∠OBD的关系,根据三角形的外角的性质,可得答案.
解答:解:∠ABC的平分线交AD于点O,
∴∠OBD=∠ABO=32°,
AD⊥BC于点D,D为BC的中点,
∴OB=OC,∠ADC=90°,
∠OCD=∠OBD=32°,
由三角形外角的性质得∠AOC=∠C+∠ADC=90°+32°=122°.
故答案为:122°.
∴∠OBD=∠ABO=32°,
AD⊥BC于点D,D为BC的中点,
∴OB=OC,∠ADC=90°,
∠OCD=∠OBD=32°,
由三角形外角的性质得∠AOC=∠C+∠ADC=90°+32°=122°.
故答案为:122°.
点评:本题考查了等腰三角形的判定与性质,利用了等腰三角形的判定与性质,三角形外角的性质.

练习册系列答案
相关题目
计算(x-a)(x2+ax+a2)的结果是( )
| A、x3+2ax2-a3 |
| B、x3-a3 |
| C、x3+2a2x-a3 |
| D、x3+2ax2+2a2x-a3 |
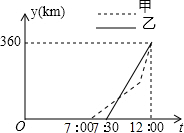 甲、乙两车从A地前往B地,甲车行至AB的中点C处后,以原来速度的1.5倍继续行驶,在整个行程中,汽车离开A地的距离y与时刻t的对应关系如图所示,求:
甲、乙两车从A地前往B地,甲车行至AB的中点C处后,以原来速度的1.5倍继续行驶,在整个行程中,汽车离开A地的距离y与时刻t的对应关系如图所示,求: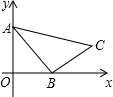 如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=
如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=