题目内容
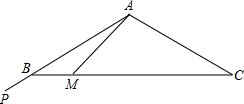 在一次科技活动中,小明进行了模拟雷达扫描实验.如图,表盘是△ABC,其中AB=AC,∠BAC=120°,在点A处有一束红外光线AP,从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.小明通过实验发现,光线从AB处旋转开始计时,旋转1秒,此时光线AP交BC边于点M,BM的长为(20
在一次科技活动中,小明进行了模拟雷达扫描实验.如图,表盘是△ABC,其中AB=AC,∠BAC=120°,在点A处有一束红外光线AP,从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.小明通过实验发现,光线从AB处旋转开始计时,旋转1秒,此时光线AP交BC边于点M,BM的长为(20| 3 |
(1)求AB的长;
(2)从AB处旋转开始计时,若旋转6秒,此时光线AP与BC边的交点在什么位置?若旋转2014秒,交点又在什么位置?请说明理由.
考点:解直角三角形的应用
专题:几何图形问题,规律型
分析:(1)如图1,过A点作AD⊥BC,垂足为D.令AB=2tcm.在Rt△ABD中,根据三角函数可得AD=
AB=t,BD=
AB=
t.在Rt∠AMD中,MD=AD=t.由BM=BD-MD,得到关于t的方程,求得t的值,从而求得AB的长;
(2)如图2,当光线旋转6秒,设AP交BC于点N,在Rt△ABN中,根据三角函数可得BN;如图3,设光线AP旋转2014秒后光线与BC的交点为Q.求得CQ=
,BC=40
.根据BQ=BC-CQ即可求解.
| 1 |
| 2 |
| ||
| 2 |
| 3 |
(2)如图2,当光线旋转6秒,设AP交BC于点N,在Rt△ABN中,根据三角函数可得BN;如图3,设光线AP旋转2014秒后光线与BC的交点为Q.求得CQ=
80
| ||
| 3 |
| 3 |
解答: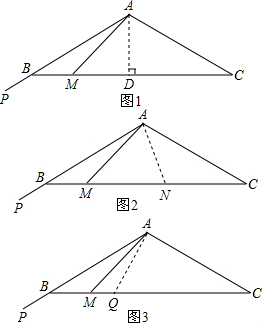 解:(1)如图1,过A点作AD⊥BC,垂足为D.
解:(1)如图1,过A点作AD⊥BC,垂足为D.
∵∠BAC=120°,AB=AC,
∴∠ABC=∠C=30°.
令AB=2tcm.
在Rt△ABD中,AD=
AB=t,BD=
AB=
t.
在Rt△AMD中,∵∠AMD=∠ABC+∠BAM=45°,
∴MD=AD=t.
∵BM=BD-MD.即
t-t=20
-20.
解得t=20.
∴AB=2×20=40cm.
答:AB的长为40cm.
(2)如图2,当光线旋转6秒,
设AP交BC于点N,此时∠BAN=15°×6=90°.
在Rt△ABN中,BN=
=
=
.
∴光线AP旋转6秒,与BC的交点N距点B
cm处.
如图3,设光线AP旋转2014秒后光线与BC的交点为Q.
由题意可知,光线从边AB开始到第一次回到AB处需8×2=16秒,
而2014=125×16+14,即AP旋转2014秒与旋转14秒时和BC的交点是同一个点Q.
旋转14s的过程是B→C:8s,C→Q:6s,因此CQ=BN=
,
∵AB=AC,∠BAC=120°,
∴BC=2ABcos30°=2×40×
=40
,
∴BQ=BC-CQ=40
-
=
,
∴光线AP旋转2014秒后,与BC的交点Q在距点B
cm处.
 解:(1)如图1,过A点作AD⊥BC,垂足为D.
解:(1)如图1,过A点作AD⊥BC,垂足为D.∵∠BAC=120°,AB=AC,
∴∠ABC=∠C=30°.
令AB=2tcm.
在Rt△ABD中,AD=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
在Rt△AMD中,∵∠AMD=∠ABC+∠BAM=45°,
∴MD=AD=t.
∵BM=BD-MD.即
| 3 |
| 3 |
解得t=20.
∴AB=2×20=40cm.
答:AB的长为40cm.
(2)如图2,当光线旋转6秒,
设AP交BC于点N,此时∠BAN=15°×6=90°.
在Rt△ABN中,BN=
| AB |
| cos30° |
| 40 | ||||
|
80
| ||
| 3 |
∴光线AP旋转6秒,与BC的交点N距点B
80
| ||
| 3 |
如图3,设光线AP旋转2014秒后光线与BC的交点为Q.
由题意可知,光线从边AB开始到第一次回到AB处需8×2=16秒,
而2014=125×16+14,即AP旋转2014秒与旋转14秒时和BC的交点是同一个点Q.
旋转14s的过程是B→C:8s,C→Q:6s,因此CQ=BN=
80
| ||
| 3 |
∵AB=AC,∠BAC=120°,
∴BC=2ABcos30°=2×40×
| ||
| 2 |
| 3 |
∴BQ=BC-CQ=40
| 3 |
80
| ||
| 3 |
40
| ||
| 3 |
∴光线AP旋转2014秒后,与BC的交点Q在距点B
40
| ||
| 3 |
点评:考查了解直角三角形的应用,主要是三角函数的基本概念及运算,注意方程思想的应用.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 如图,已知直线a∥b,∠1=120°,则∠2的度数是
如图,已知直线a∥b,∠1=120°,则∠2的度数是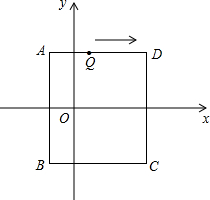 如图,在平面直角坐标系中,长方形ABCD的边BC∥x轴.如果A点坐标是(
如图,在平面直角坐标系中,长方形ABCD的边BC∥x轴.如果A点坐标是( 如图,AC⊥BC于点C,DE⊥BE于点E,BC平分∠ABE,∠BDE=58°.则∠A=
如图,AC⊥BC于点C,DE⊥BE于点E,BC平分∠ABE,∠BDE=58°.则∠A=