题目内容
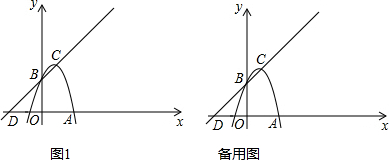
5.【问题背景】已知:正方形ABCD的边长为1,点E是射线BC上一点,点F为射线CD上一点,∠EAF大小始终等于45°.
【先易后难】如图1,当点E在边BC上时,延长EB到F′,使BF′=DF,连接AF′.求证:EF′=EF.
【动中求静】当点E在BC延长线上时,直接写出BE,EF,DF三者之间的数量关系,不必证明.
【拓展探究】当点E在BC延长线上时,设AE与CD交于点G,如图2.问△EGF与△EFA能否相似?若能相似,求出BE的值;若不可能相似,请说明理由.
分析 【先易后难】由正方形的性质得出AB=AD,∠BAD=∠D=∠ABC=∠ABF′=90°,由SAS证明△ABF′≌△ADF,得出∠BAF′=∠DAF,AF′=AF,证出∠EAF′=∠EAF,由SAS证明△EAF′≌△EAF,得出对应边相等即可.
【动中求静】同上类似得出BE=EF+DF.
【拓展探究】△EGF与△EFA相似;只需∠EFG=∠EAF=45°,此时由CF=CE,设BE=x,DF=y,由BE=EF+DF得出EF=x-y,由勾股定理得出(x-1)2+(1+y)2=(x-y)2,得出y=$\frac{x-1}{x+1}$(x>1),由CF=CE,得出方程,解方程即可.
解答 【先易后难】解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠D=∠ABC=∠ABF′=90°,
在△ABF′和△ADF中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠ABF′=∠D}&{\;}\\{BD′=DF}&{\;}\end{array}\right.$,
∴△ABF′≌△ADF(SAS),
∴∠BAF′=∠DAF,AF′=AF,
∵∠EAF=45°,
∴∠BAE+∠DAF=90°-45°=45°,
∴∠BAE+∠BAF′=45°,
即∠EAF′=45°=∠EAF,
在△EAF′和△EAF中,$\left\{\begin{array}{l}{AF′=AF}&{\;}\\{∠EAF′=∠EAF}&{\;}\\{AE=AE}&{\;}\end{array}\right.$,
∴△EAF′≌△EAF(SAS),
∴EF′=EF.
【动中求静】解:BE=EF+DF.
【拓展探究】解:△EGF与△EFA能相似;
∵∠GEF=∠FEA,
∴当∠EFG=∠EAF=45°时,△EGF与△EFA相似;
此时由CF=CE,
设BE=x,DF=y,
由(2)得:EF=x-y,
∵∠ECF=∠BCD=90°,
∴CE2+CF2=EF2,
即(x-1)2+(1+y)2=(x-y)2,
化简得:y=$\frac{x-1}{x+1}$(x>1),
∵CF=CE,
∴x-1=1+y,
即x-1=1+$\frac{x-1}{x+1}$,
化简得:x2-2x-1=0,
解得:x=1±$\sqrt{2}$(负值舍去),
∴BE=1+$\sqrt{2}$.
点评 本题是相似形综合题目,考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理等知识;本题综合性强,有一定难度,证明三角形全等和三角形相似是解决问题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | -3或5 | B. | 3或-5 | C. | -3或3 | D. | -5或5 |
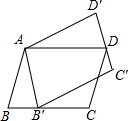 如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )
如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )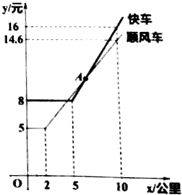 随着互联网的发展,互联网消费逐渐深入人们生活,如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,下列说法:
随着互联网的发展,互联网消费逐渐深入人们生活,如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,下列说法: