��Ŀ����
����Ŀ����֪������![]() ��
��![]() ����������
����������![]() ����
����![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ʱ����1��������
ʱ����1��������![]() ��
��![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ��
��![]() �������������ƣ�
�������������ƣ�
��1����![]() ��
��![]() ��ֵ��������
��ֵ��������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2��������![]() �Ķ���
�Ķ���![]() ������Ϊ�� �� �����������ƣ���
������Ϊ�� �� �����������ƣ���![]() ��������
��������![]() �Ķ���
�Ķ���![]() ������Ϊ�� �� �������������ߵĶ�����������ĺ�����ϵʽ�� ��
������Ϊ�� �� �������������ߵĶ�����������ĺ�����ϵʽ�� ��
��3��̽�����н��ۣ�
���Ƿ����������![]() ��ʹ��
��ʹ��![]() Ϊ����ֱ�������Σ������ڣ�����������ߵı���ʽ���������ڣ���˵�����ɣ�
Ϊ����ֱ�������Σ������ڣ�����������ߵı���ʽ���������ڣ���˵�����ɣ�
����ֱ��![]() ��������
��������![]() �ֱ������߶�
�ֱ������߶�![]() ��
��![]() ����
����![]() ���߶�
���߶�![]() ��
��![]() ����
����![]() �ij��кι��ɣ����ú�
�ij��кι��ɣ����ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
���𰸡���1��![]() ��
��![]() ��
��![]() ����2��3��9��
����2��3��9��![]() ��
��![]() ��
��![]() ����3���ٴ��ڣ�
����3���ٴ��ڣ�![]() ����
����![]() ��
��
��������
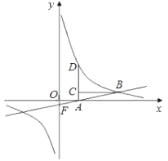
(1)A1(2��0)����C1=2����C2=2+2=4������A��A1��������������߱���ʽ�����![]() ��
��![]() ����A1(2��0)����C1=2����C2=2+2=4��������ô𰸣�
����A1(2��0)����C1=2����C2=2+2=4��������ô𰸣�
(2)ͬ���ɵã�a3=3��b3=9�������Ƴ���![]() ������Ϊ(n��n2)�������������ߵĶ�����������ĺ�����ϵʽ�ǣ�y=x2��������⣻
������Ϊ(n��n2)�������������ߵĶ�����������ĺ�����ϵʽ�ǣ�y=x2��������⣻
(3)�١�AAnBnΪ����ֱ�������Σ���AAn2=2ABn2����(2n)2=2(n2+n4)��������⣻
���������![]() ��
��![]() �����
����� ![]() ��������⣮
��������⣮
(1)��![]() ʱ����1��������
ʱ����1��������![]() ��
��![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��֪��
��֪��![]() ��
��
��������![]() ��
��![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ��
��![]() ��
��
![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��![]() ��
��
(2)ͬ���ɵã�������![]() ��
��![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ��
��![]() ��
��
![]() ��
��
��a3=3��b3=9��
![]() ��
��
�����Ƴ�����![]() (n��n2)��
(n��n2)��
�����������ߵĶ�����������ĺ�����ϵʽ�ǣ�y=x2��
�ʴ�Ϊ�� 3��9��![]() ��
��![]() ��
��![]() ��
��
(3)�ٴ��ڣ���(1)��(2)��![]() ��
��![]() ��
��
��![]() Ϊ����ֱ�������Σ���AAn2=2ABn2����
Ϊ����ֱ�������Σ���AAn2=2ABn2����![]() ��
��
��![]() ��
��
���![]() ��
��![]() (��ȥ)
(��ȥ)
�����������![]() ʹ��
ʹ��![]() Ϊ����ֱ�������Σ�
Ϊ����ֱ�������Σ�
��ʱ������Ϊ��![]()
�ڡ�![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��