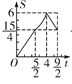题目内容
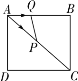
【题目】如图，已知△ABC，∠B=90゜，AB=3，BC=6，动点P、Q同时从点B出发，动点P沿BA以1个单位长度/秒的速度向点A移动，动点Q沿BC以2个单位长度/秒的速度向点C移动，运动时间为t秒．连接PQ，将△QBP绕点Q顺时针旋转90°得到△
，设△与△ABC重合部分面积是S．
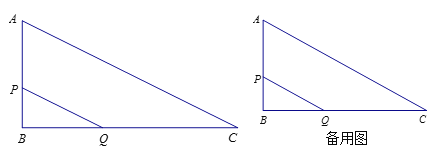
（1）求证：PQ∥AC；
（2）求S与t的函数关系式，并直接写出自变量t的取值范围．
【答案】（1）见解析；（2）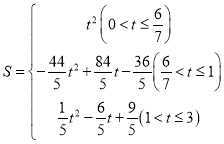
【解析】
（1）由题意可得出
，继而可证明△BPQ∽△BAC，从而证明结论；
（2）由题意得出QP`⊥AC，分三种情况利用相似三角形的判定及性质讨论计算．
解：（1）∵BP=t，BQ=2t，AB=3，BC=6
∴
∵∠B=∠B
∴△BPQ∽△BAC
∴∠BPQ=∠A
∴PQ∥AC
（2）∵BP=t
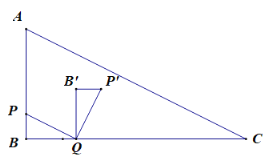
BQ=2t
∴P`Q=
∵AB=3 BC=6
∴AC=3
∵PQ∥AC
∴QP`⊥AC
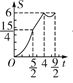
当0<t≤
时，S=t2
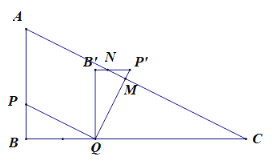
当<t≤1时：
设QP`交AC于点M
P`B`交AC于点N
∴∠QMC=∠B=90°
∴△QMC∽△ABC
∴
∴
∴QM=
∵P`Q=t
∴P`M= 
又∵∠P`=∠BPQ=∠A
∴△P`NM∽△ACB
∴
∴MN=2P`M
∴S△P`MN=
P`M·MN=P`M2=
∴
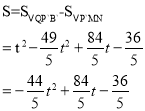
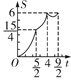
当1<t≤3时
设QB`交AC于点H
∵∠HQM=∠PQB
∴△HMQ∽△PBQ
∴
∴MH=MQ
∴
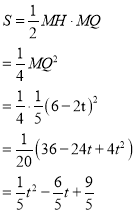
综合上所述：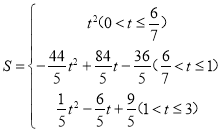
练习册系列答案
名校课堂系列答案
相关题目
