题目内容
10. 如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.
如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.(1)求⊙O的半径;
(2)点E为圆上一点,∠ECD=15°,将$\widehat{CE}$沿弦CE翻折,交CD于点F,求图中阴影部分的面积.
分析 (1)根据AB⊥CD,垂足为G,OG:OC=3:5,AB=8,可以求得⊙O的半径;
(2)要求阴影部分的面积只要做出合适的辅助线,然后利用锐角三角函数、扇形的面积和三角形的面积即可解答本题.
解答 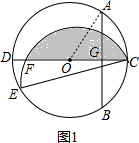 解:(1)连接AO,如右图1所示,
解:(1)连接AO,如右图1所示,
∵CD为⊙O的直径,AB⊥CD,AB=8,
∴AG=$\frac{1}{2}AB$=4,
∵OG:OC=3:5,AB⊥CD,垂足为G,
∴设⊙O的半径为5k,则OG=3k,
∴(3k)2+42=(5k)2,
解得,k=1或k=-1(舍去),
∴5k=5,
即⊙O的半径是5;
(2)如图2所示,将阴影部分沿CE翻折,点F的对应点为M,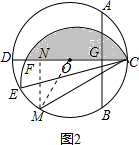
∵∠ECD=15°,由对称性可知,∠DCM=30°,S阴影=S弓形CBM,
连接OM,则∠MOD=60°,
∴∠MOC=120°,
过点M作MN⊥CD于点N,
∴MN=MO•sin60°=5×$\frac{\sqrt{3}}{2}=\frac{5\sqrt{3}}{2}$,
∴S阴影=S扇形OMC-S△OMC=$\frac{120×π×{5}^{2}}{360}-\frac{1}{2}×5×\frac{5\sqrt{3}}{2}$=$\frac{25π}{3}-\frac{25\sqrt{3}}{4}$,
即图中阴影部分的面积是:$\frac{25π}{3}-\frac{25\sqrt{3}}{4}$.
点评 本题考查垂径定理、扇形的面积、翻折变换,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
20.下列计算正确的是( )
| A. | 2a3+3a3=5a6 | B. | (x5)3=x8 | ||
| C. | -2m(m-3)=-2m2-6m | D. | (-3a-2)(-3a+2)=9a2-4 |
18.第31届夏季奥运会将于2016年8月5日-21日在巴西举行,为纪念此次体育盛事发行的奥运会纪念币,在中国发行450000套,450000这个数用科学记数法表示为( )
| A. | 45×104 | B. | 4.5×105 | C. | 0.45×106 | D. | 4.5×106 |
10.若a>1,则1+$\frac{\sqrt{(1-a)^{2}}}{a-1}$的值是( )
| A. | 1 | B. | 2 | C. | 0 | D. | -1 |
7.已知a和b是有理数,若a+b=0,ab≠0,则在a和b之间一定( )
| A. | 存在负整数 | B. | 存在正整数 | C. | 存在负分数 | D. | 不存在正分数 |
 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,其限制电流不能超过10A,那么用电器可变电阻R应控制的范围是R≥3.6.
已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,其限制电流不能超过10A,那么用电器可变电阻R应控制的范围是R≥3.6.