题目内容
6.把下列各式分解因式:(1)8m2n+2mn;
(2)-4a3+16a2-18a;
(3)-3a2b2+6ab2c-9abc;
(4)p(a2+b2)-q(a2+b2);
(5)2a2(b-c)+3a(c-b);
(6)m2(a-2)+m(2-a);
(7)20×(-3)2+60×(-3);
(8)572+2×57×43+432.
分析 (1)原式提取公因式即可得到结果;
(2)原式提取公因式即可得到结果;
(3)原式提取公因式即可得到结果;
(4)原式提取公因式即可得到结果;
(5)原式变形后,提取公因式即可得到结果;
(6)原式变形后,提取公因式即可得到结果;
(7)原式提取公因式即可得到结果;
(8)原式利用完全平方公式变形,计算即可得到结果.
解答 解:(1)8m2n+2mn=2mn(4m+1);
(2)-4a3+16a2-18a=-2a(2a2-8a+9);
(3)-3a2b2+6ab2c-9abc=-3ab(ab+2b+3);
(4)p(a2+b2)-q(a2+b2)=(a2+b2)(p-q);
(5)2a2(b-c)+3a(c-b)=a(b-c)(2a-3);
(6)m2(a-2)+m(2-a)=m(a-2)(m-1);
(7)20×(-3)2+60×(-3)=20×(-3)×(-3+3)=0;
(8)572+2×57×43+432=(57+43)2=1002=10000.
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.长为9,6,5,3的四根木条,选其中三根,共可以组成三角形( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
11. 如图,△ABC中,AB=AC=13,BC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
如图,△ABC中,AB=AC=13,BC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
 如图,△ABC中,AB=AC=13,BC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
如图,△ABC中,AB=AC=13,BC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )| A. | 16.5 | B. | 18 | C. | 23 | D. | 26 |
18.0.04的算术平方根是( )
| A. | 0.02 | B. | 0.2 | C. | -0.2 | D. | ±0.2 |
15.一组数据的方差为s2,将这组数据的每个数据都扩大三倍,所得到的一组新的数据的方差为( )
| A. | 9s2 | B. | s2 | C. | 3s2 | D. | 2s2 |
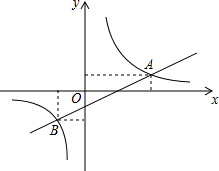 如图,反比例函数y=$\frac{k}{x}$(k≠0)和一次函数y=ax+b(a≠0)的图象交于A(4,$\frac{3}{2}$),B(-2,n) 两点.
如图,反比例函数y=$\frac{k}{x}$(k≠0)和一次函数y=ax+b(a≠0)的图象交于A(4,$\frac{3}{2}$),B(-2,n) 两点. 如图,将△ABC绕点A按顺时针方向旋转60°得△ADE,则∠BAD=60度.
如图,将△ABC绕点A按顺时针方向旋转60°得△ADE,则∠BAD=60度.