题目内容
10. 在△ABC中,∠ADC=∠ACB,AD=9,DB=3,求AC的长.
在△ABC中,∠ADC=∠ACB,AD=9,DB=3,求AC的长.
分析 先根据已知条件求证出△ADC∽△ACB,再根据三角形的相似比求解.
解答 解:∵∠ADC=∠ACB,∠A=∠A,
∴△ADC∽△ACB,
∴$\frac{AD}{AC}=\frac{AC}{AB}$,即$\frac{9}{AC}=\frac{AC}{12}$,
∴AC=$\sqrt{9×12}$=6$\sqrt{3}$.
点评 本题考查的是相似三角形的性质和判定,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
18.如图,下列四个几何体,从上面、正面、左侧三个不同方向看到的形状中只有两个相同的是( )
| A. |  正方体 | B. |  球 | C. |  直三棱柱 | D. |  圆柱 |
20.关于x的方程x2+(2a2+a-$\sqrt{2{a}^{2}+a+6}$)x+a=0的两实数根互为相反数,则a=( )
| A. | -$\frac{3}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
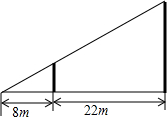 如图,小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m、与旗杆相距22m,求旗杆的高度.
如图,小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m、与旗杆相距22m,求旗杆的高度. 如图所示,电镀螺杆呈现出了两个几何体的组合,则这个两个几何体分别是圆柱、六棱柱.
如图所示,电镀螺杆呈现出了两个几何体的组合,则这个两个几何体分别是圆柱、六棱柱.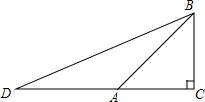 如图,在△ABC中,∠C=90°,AC=BC,延长CA到D使AD=AB,
如图,在△ABC中,∠C=90°,AC=BC,延长CA到D使AD=AB,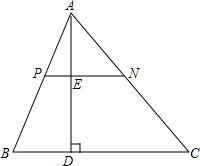 已知:如图所示,PN∥BC,AD⊥BC交PN于点E,交BC于点D.
已知:如图所示,PN∥BC,AD⊥BC交PN于点E,交BC于点D. 如图,AB∥CD,点E在BC上,∠BED=68°,∠D=38°,则∠B的度数为30°.
如图,AB∥CD,点E在BC上,∠BED=68°,∠D=38°,则∠B的度数为30°.