题目内容
15.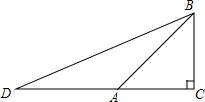 如图,在△ABC中,∠C=90°,AC=BC,延长CA到D使AD=AB,
如图,在△ABC中,∠C=90°,AC=BC,延长CA到D使AD=AB,(1)求∠D的度数;
(2)求tan∠D的值;
(3)计算tan∠DBC的值.
分析 (1)先求得∠BAC=45°,然后由等腰三角形的性质和三角形的外角的性质可知∠D=$\frac{1}{2}∠BAC$;
(2)由特殊锐角三角函数可知:AB=$\sqrt{2}BC$,然后可知DC=AC+AD=BC+$\sqrt{2}$CB,最后根据正切函数的定义求解即可;
(3)由锐角三角函数的定义求解即可.
解答 解:(1)∵∠C=90°,AC=BC,
∴∠BAC=45°.
∵AD=AB,
∴∠BDA=∠DBA.
由三角形的外角的性质可知:∠BDA+∠DBA=45°.
∴2∠D=45°.
∴∠D=22.5°.
(2)在Rt△ABC中,∠BAC=45°,
∴$\frac{BC}{AB}=\frac{\sqrt{2}}{2}$.
∴AB=$\sqrt{2}$CB.
∵AD=AB,
∴AD=$\sqrt{2}$BC.
∴tan∠D=$\frac{BC}{DC}$=$\frac{BC}{(1+\sqrt{2})CB}$=$\sqrt{2}-1$.
(3)tan∠DBC=$\frac{DC}{BC}$=1+$\sqrt{2}$.
点评 本题主要考查的是解直角三角形、特殊锐角三角函数值、等腰三角形的性质、三角形外角的性质、熟练掌握相关知识是解题的关键.

练习册系列答案
相关题目
7.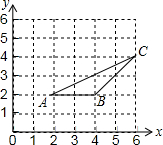 如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点0为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为( )
如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点0为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为( )
 如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点0为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为( )
如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点0为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为( )| A. | (2,$\frac{3}{2}$) | B. | (-2,-$\frac{3}{2}$) | C. | (2,$\frac{3}{2}$)或(-2,-$\frac{3}{2}$) | D. | (8,6)或(-8,-6) |
5.在一次质检抽测中,随机抽取某摊位10袋食盐,测得各袋的质量分别为(单位:g)
501,502,504,496,497,503,496,500,501,499
根据以上抽测结果,任买一袋该摊位的食盐,质量在497.5g~501.5g之间的概率为( )
501,502,504,496,497,503,496,500,501,499
根据以上抽测结果,任买一袋该摊位的食盐,质量在497.5g~501.5g之间的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
 如图,在△ABC中,AB>AC,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于F,交AB、AC于E、G.
如图,在△ABC中,AB>AC,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于F,交AB、AC于E、G. 在△ABC中,∠ADC=∠ACB,AD=9,DB=3,求AC的长.
在△ABC中,∠ADC=∠ACB,AD=9,DB=3,求AC的长.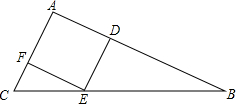 △ABC的边AB=6,AC=4,若菱形DEFA内接于△ABC,则菱形的边长为2.4.
△ABC的边AB=6,AC=4,若菱形DEFA内接于△ABC,则菱形的边长为2.4.