题目内容
7.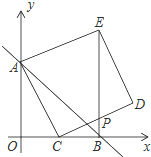 在平面直角坐标系中,直线AB与两坐标轴的交点分别是A(0,3)、B(3,0),C为线段OB上一动点,以AC为边向右作正方形ACDE,连接EB,EB与CD相交于点P.
在平面直角坐标系中,直线AB与两坐标轴的交点分别是A(0,3)、B(3,0),C为线段OB上一动点,以AC为边向右作正方形ACDE,连接EB,EB与CD相交于点P.(1)求直线AB的解析式;
(2)证明:BE⊥BC;
(3)求点P到达最高位置时的坐标.
分析 (1)首先设直线AB的解析式为:y=kx+b,由直线AB与两坐标轴的交点分别是A(0,3),B(3,0),利用待定系数法即可求得直线AB的解析式;
(2)首先过点E作EF⊥y轴于点F,易证得△AEF≌△CAO(AAS),则可证得四边形OBEF是矩形,则可得BE⊥BO;
(3)首先设点C(a,0),则可得OC=a,BC=OB-OC=3-a,易证得△OAC∽△BCP,然后由相似三角形的对应边成比例,求得PB=-$\frac{1}{3}$a2+a=-$\frac{1}{3}$(a-$\frac{3}{2}$)2+$\frac{3}{4}$,继而求得答案.
解答 解:(1)设直线AB的解析式为:y=kx+b,
∵直线AB与两坐标轴的交点分别是A(0,3),B(3,0),
∴$\left\{\begin{array}{l}{b=3}\\{3k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=3}\\{k=-1}\end{array}\right.$,
∴直线AB的解析式为:y=-x+3; (2)过点E作EF⊥y轴于点F,
(2)过点E作EF⊥y轴于点F,
∵四边形ACDE是正方形,
∴AC=AE,∠EAC=90°,
∴∠EAF+∠OAC=90°,
∵∠OAC+∠ACO=90°,
∴∠EAF=∠ACO,
在△AEF和△CAO中,
$\left\{\begin{array}{l}{∠AFE=∠COA=90°}\\{∠EAF=∠ACO}\\{AE=CA}\end{array}\right.$,
∴△AEF≌△CAO(AAS),
∴EF=OA=4,AF=OC,
∴EF=OB,
∵EF∥OB,
∴四边形OBEF是平行四边形,
∵∠FOB=90°,
∴四边形OBEF是矩形,
∴BE⊥BO;
(3)∵∠ACD=90°,
∴∠ACO+∠BCP=90°,
∵∠ACO+∠OAC=90°,
∴∠BCP=∠OAC,
∵∠AOC=∠CBP=90°,
∴△OAC∽△BCP,
∴$\frac{OA}{BC}$=$\frac{OC}{BP}$,
设点C(a,0),
则OC=a,BC=OB-OC=3-a,
∴$\frac{3}{3-a}$=$\frac{a}{PB}$,
∴PB=-$\frac{1}{3}$a2+a=-$\frac{1}{3}$(a-$\frac{3}{2}$)2+$\frac{3}{4}$,
∴当a=$\frac{3}{2}$时,PB最大,最大值为$\frac{3}{4}$,
∴点P到达最高位置时的坐标为:(3,$\frac{3}{4}$).
点评 此题属于一次函数的综合题,考查了待定系数法求函数的解析式、全等三角形的判定与性质、相似三角形的判定与性质以及二次函数的最值问题.此题难度较大,注意掌握数形结合思想与方程思想的应用.

 阅读快车系列答案
阅读快车系列答案| A. | 第二象限内 | B. | 第一或第三象限内 | ||
| C. | 第二或第四象限内 | D. | 第四象限 |
 已知a,b,c在数轴上的位置如图所示,则( )
已知a,b,c在数轴上的位置如图所示,则( )| A. | |a|<|b|<|c| | B. | |a|>|b|>|c| | C. | |a|>|c|>|b| | D. | |c|>|a|>|b| |
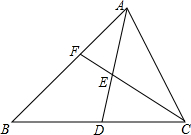 如图△ABC中,AD为中线,求证:AE:ED=2AF:FB.
如图△ABC中,AD为中线,求证:AE:ED=2AF:FB. 如图是具有互为相反数的三角形数阵.当最下面一行的两个数为多少时,这两个数以及它们上面的数的个数为2013.
如图是具有互为相反数的三角形数阵.当最下面一行的两个数为多少时,这两个数以及它们上面的数的个数为2013.