题目内容
11.已知m2+m-1=0,求$\frac{2}{{m}^{2}+m}$-$\frac{m+2}{{m}^{2}+2m+1}$的值.分析 原式通分并利用同分母分式的减法法则计算,将已知等式变形后代入计算即可求出值.
解答 解:∵m2+m-1=0,即m2=1-m,m2+m=1,
∴原式=$\frac{2}{m(m+1)}$-$\frac{m+2}{(m+1)^{2}}$=$\frac{2(m+1)-m(m+2)}{m(m+1)^{2}}$=$\frac{2-{m}^{2}}{m(m+1)^{2}}$=$\frac{m+1}{m(m+1)^{2}}$=$\frac{1}{{m}^{2}+m}$=1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
19.下列说法中,正确的是( )
| A. | “打开电视机,正在播放体育节目”是必然事件 | |
| B. | 检测某校早餐奶的质量,应该采用抽样调查的方式 | |
| C. | 某同学连续10次投掷质量均匀的硬币,3次正面向上,因此正面向上的概率是30% | |
| D. | 在连续5次数学测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定 |
3.某班组织了一次读书活动,统计了10名同学在一周内累计的读书时间,如表所示,对于这10个同学的一周累计读书时间,下列说法错误的是( )
| 一周内累计的读书时间(小时) | 6 | 8 | 10 | 11 |
| 人数(个) | 1 | 4 | 3 | 2 |
| A. | 众数是8 | B. | 中位数是9 | C. | 平均数是9 | D. | 方差是1.5 |
1.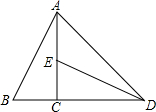 如图所示,将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,连接AD,若∠BAC=25°,则∠ADE=( )
如图所示,将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,连接AD,若∠BAC=25°,则∠ADE=( )
 如图所示,将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,连接AD,若∠BAC=25°,则∠ADE=( )
如图所示,将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,连接AD,若∠BAC=25°,则∠ADE=( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
 如图,E、F是平行四边形ABCD的对角线AC上两点,且BE∥DF,求证:四边形BFED是平行四边形.
如图,E、F是平行四边形ABCD的对角线AC上两点,且BE∥DF,求证:四边形BFED是平行四边形. 我们把:“有一组邻角相等的凸四边形”叫做“等邻角四边形”.
我们把:“有一组邻角相等的凸四边形”叫做“等邻角四边形”.