题目内容
20.已知,关于x的方程x2-4x+3-k=0.(1)当k为何值时方程有两个不相等的实数根;
(2)若方程有一根2+$\sqrt{3}$,求k的值及方程的另一根.
分析 (1)先求出△,再根据根的判别式即可求出k的值;
(2)先把x=2+$\sqrt{3}$代入方程可计算出k,然后利用根与系数的关系计算出另一个根即可.
解答 解:(1)该方程的判别式为:△=(-4)2-4(3-k)=4+4k,
∵方程有两个不相等的实数根,
∴4+4k>0,
解得:k>-1;
∴当k>-1时方程有两个不相等的实数根;
(2)把x=2+$\sqrt{3}$代入方程得:(2+$\sqrt{3}$)2-4(2+$\sqrt{3}$)+3-k=0.
解得k=2,
设方程另一个根为t,
则2$+\sqrt{3}$+t=4,
解得:t=2-$\sqrt{3}$,
即另一根为2-$\sqrt{3}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的解和根与系数的关系.

练习册系列答案
相关题目
11.计算7-4的结果是( )
| A. | 3 | B. | -3 | C. | 11 | D. | -11 |
8.下列命题中,真命题有( )
①点P(a,a)一定在第一象限角平分线上;
②点P(-a,-a)一定在第二象限的角平分线上;
③点P(x,y)关于x轴的对称点是(x,-y);
④点M(3,-2)到x轴的距离是3,到y轴的距离是2.
①点P(a,a)一定在第一象限角平分线上;
②点P(-a,-a)一定在第二象限的角平分线上;
③点P(x,y)关于x轴的对称点是(x,-y);
④点M(3,-2)到x轴的距离是3,到y轴的距离是2.
| A. | 0 个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.下列说法中能确定平面点的位置的正确说法有几种( )
①一对有序实数对
②到原点的距离为5北偏东45°的方向
③到原点的距离为5,西南方向
④东偏南37°
⑤北纬40o,东经116o.
①一对有序实数对
②到原点的距离为5北偏东45°的方向
③到原点的距离为5,西南方向
④东偏南37°
⑤北纬40o,东经116o.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
9.将一个圆形经过平移后再旋转得到另一个圆形,则这两个图形( )
| A. | 大小改变 | B. | 形状改变 | C. | 位置不变 | D. | 大小不变 |
10.与$\sqrt{24}$最接近的整数是( )
| A. | 2 | B. | 6 | C. | 4 | D. | 5 |
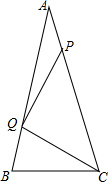 如图所示,在△ABC中,AB=AC,∠BAC=30°,P、Q分别为AB、AC的点,且∠QPC=45°,PQ=BC,证明:BC=CQ.
如图所示,在△ABC中,AB=AC,∠BAC=30°,P、Q分别为AB、AC的点,且∠QPC=45°,PQ=BC,证明:BC=CQ.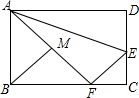 如图,在矩形ABCD中,AD=10,CD=6,E是CD边上一点,沿AE折叠△ADE,使点D恰好落在BC边上的F处,则$\frac{BF}{AF}$=$\frac{4}{5}$.
如图,在矩形ABCD中,AD=10,CD=6,E是CD边上一点,沿AE折叠△ADE,使点D恰好落在BC边上的F处,则$\frac{BF}{AF}$=$\frac{4}{5}$.