题目内容
如图,在等腰直角三角形ABC中,AC=BC=6cm,正方形DEFG的边长是2cm.其中边EF在BC所在的直线a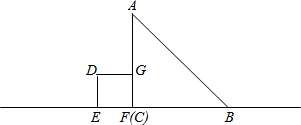 上,开始时,点F和点C重合,让正方形DEFG沿直线a向右以每秒1cm的速度匀速运动,直至点E与点B重合时停止运动.
上,开始时,点F和点C重合,让正方形DEFG沿直线a向右以每秒1cm的速度匀速运动,直至点E与点B重合时停止运动.
(1)请直接写出正方形运动6秒时,与△ABC重叠部分面积的大小;
(2)设运动时间为x(秒),运动过程中正方形DEFG与△ABC重叠部分的面积为y(cm2)
①x在什么范围内,y的值不随x的变化而变化?
②在运动过程中,当x为何值时,y=
.
 上,开始时,点F和点C重合,让正方形DEFG沿直线a向右以每秒1cm的速度匀速运动,直至点E与点B重合时停止运动.
上,开始时,点F和点C重合,让正方形DEFG沿直线a向右以每秒1cm的速度匀速运动,直至点E与点B重合时停止运动.(1)请直接写出正方形运动6秒时,与△ABC重叠部分面积的大小;
(2)设运动时间为x(秒),运动过程中正方形DEFG与△ABC重叠部分的面积为y(cm2)
①x在什么范围内,y的值不随x的变化而变化?
②在运动过程中,当x为何值时,y=
| 1 |
| 2 |
考点:相似形综合题
专题:
分析:(1)根据题意画出图形,再根据已知条件可直接得出与△ABC重叠部分面积S=
×2×2,再进行整理即可;
(2)①设运动时间为x(秒),画出图形,根据当2≤x≤4时正方形DEFG与△ABC重叠部分的面积y=正方形DEFG的面积,y的值不随x的变化而变化;
②分两种情况进行讨论,当0<x<2时正方形DEFG与△ABC重叠部分的面积y=CF•GF,当6<x<8时正方形DEFG与△ABC重叠部分的面积y=
BE2,分别列出方程求解即可.
| 1 |
| 2 |
(2)①设运动时间为x(秒),画出图形,根据当2≤x≤4时正方形DEFG与△ABC重叠部分的面积y=正方形DEFG的面积,y的值不随x的变化而变化;
②分两种情况进行讨论,当0<x<2时正方形DEFG与△ABC重叠部分的面积y=CF•GF,当6<x<8时正方形DEFG与△ABC重叠部分的面积y=
| 1 |
| 2 |
解答:解:(1)根据题意画图如下:

当正方形运动6秒时,与△ABC重叠部分面积S=
×2×2=2(cm2);
(2)①设运动时间为x(秒),如图:

当2≤x≤4时正方形DEFG与△ABC重叠部分的面积y=正方形DEFG的面积=22=4(cm2),y的值不随x的变化而变化;
②如图:

当0<x<2时正方形DEFG与△ABC重叠部分的面积y=CF•GF=x•2=2x=
,
解得:x=
,

当6<x<8时正方形DEFG与△ABC重叠部分的面积y=
BE2=
×(x-6)2=
,
解得:x=7或x=5(舍去).

当正方形运动6秒时,与△ABC重叠部分面积S=
| 1 |
| 2 |
(2)①设运动时间为x(秒),如图:

当2≤x≤4时正方形DEFG与△ABC重叠部分的面积y=正方形DEFG的面积=22=4(cm2),y的值不随x的变化而变化;
②如图:

当0<x<2时正方形DEFG与△ABC重叠部分的面积y=CF•GF=x•2=2x=
| 1 |
| 2 |
解得:x=
| 1 |
| 4 |

当6<x<8时正方形DEFG与△ABC重叠部分的面积y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:x=7或x=5(舍去).
点评:此题考查了相似形综合,用到的知识点是正方形的性质和面积、矩形和等腰直角三角形的面积,关键是根据题意画出图形,注意分两种情况讨论.

练习册系列答案
相关题目
数学小组长到书店替同学们购买数学课外资料,A种资料买了3本,每本a元,B种资料买了2本,每本b元,为了鼓励该同学,书店按两种书价的平均价即每本
元出售给这个小组长,回校后小组长按书的原价卖给了五位同学,结果发现自已正好赚回了车费;其原因是( )
| a+b |
| 2 |
| A、a>b | B、a=b |
| C、a<b | D、与a和b的大小无关 |
 已知二次函数y=ax2+bx+c的图象如图,下列结论中,正确的结论的个数有( )
已知二次函数y=ax2+bx+c的图象如图,下列结论中,正确的结论的个数有( )  如图,ABCD是一个四边形木框,为了使它保持稳定的形状,需在AC或BD上钉上一根木条,现量得AB=80cm,BC=60cm,CD=40cm,AD=50cm,试问所需的木条长度至少要多长?
如图,ABCD是一个四边形木框,为了使它保持稳定的形状,需在AC或BD上钉上一根木条,现量得AB=80cm,BC=60cm,CD=40cm,AD=50cm,试问所需的木条长度至少要多长?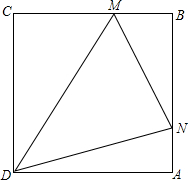 已知,边长为a(cm)的正方形ABCD,现有∠MDN=45°,其两边分别与CB、AB交与点M、N,连接MN,将∠MDN绕着顶点D旋转且使得M、N始终在边CB和边AB上,试判断在这一过程中,△BMN的周长是否发生变化,若没有变化,请求出其周长;若发生变化,请说明理由.
已知,边长为a(cm)的正方形ABCD,现有∠MDN=45°,其两边分别与CB、AB交与点M、N,连接MN,将∠MDN绕着顶点D旋转且使得M、N始终在边CB和边AB上,试判断在这一过程中,△BMN的周长是否发生变化,若没有变化,请求出其周长;若发生变化,请说明理由.