题目内容
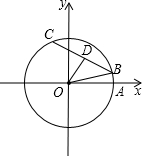 如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx-3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( )
如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx-3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( )| A、22 | ||
| B、24 | ||
C、10
| ||
D、12
|
考点:圆的综合题
专题:
分析:易知直线y=kx-3k+4过定点D(3,4),运用勾股定理可求出OD,由条件可求出半径OB,由于过圆内定点D的所有弦中,与OD垂直的弦最短,因此只需运用垂径定理及勾股定理就可解决问题.
解答:解:对于直线y=kx-3k+4,当x=3时,y=4,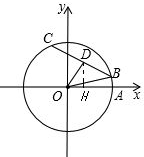
故直线y=kx-3k+4恒经过点(3,4),记为点D.
过点D作DH⊥x轴于点H,
则有OH=3,DH=4,OD=
=5.
∵点A(13,0),
∴OA=13,
∴OB=OA=13.
由于过圆内定点D的所有弦中,与OD垂直的弦最短,如图所示,
因此运用垂径定理及勾股定理可得:
BC的最小值为2BD=2
=2×
=2×12=24.
故选:B.

故直线y=kx-3k+4恒经过点(3,4),记为点D.
过点D作DH⊥x轴于点H,
则有OH=3,DH=4,OD=
| OH2+DH2 |
∵点A(13,0),
∴OA=13,
∴OB=OA=13.
由于过圆内定点D的所有弦中,与OD垂直的弦最短,如图所示,
因此运用垂径定理及勾股定理可得:
BC的最小值为2BD=2
| OB2-OD2 |
| 132-52 |
故选:B.
点评:本题主要考查了直线上点的坐标特征、垂径定理、勾股定理等知识,发现直线恒经过点(3,4)以及运用“过圆内定点D的所有弦中,与OD垂直的弦最短”这个经验是解决该选择题的关键.

练习册系列答案
相关题目
 已知⊙O的半径为5,△ABC是⊙O的内接三角形,AD是△ABC的高,且AC=4.
已知⊙O的半径为5,△ABC是⊙O的内接三角形,AD是△ABC的高,且AC=4.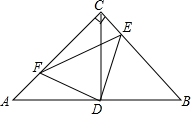 如图,在等腰Rt△ABC中,∠ACB=90°,D是AB边上的中点,点E、F分别在BC、AC边上运动,且保持AF=CE,连接DE,DF,EF,CD
如图,在等腰Rt△ABC中,∠ACB=90°,D是AB边上的中点,点E、F分别在BC、AC边上运动,且保持AF=CE,连接DE,DF,EF,CD 如图,是某宾馆楼梯示意图(一楼至二楼),若要将此楼梯铺上地毯,则至少需要
如图,是某宾馆楼梯示意图(一楼至二楼),若要将此楼梯铺上地毯,则至少需要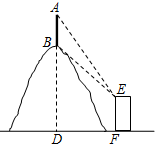 如图,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观测点E到地面的距离EF=35m,求小山BD的高.(结果保留根号)
如图,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观测点E到地面的距离EF=35m,求小山BD的高.(结果保留根号) 如图,△ABC内接于⊙O,AB=8,AC=6,D是AB边上的一点,P是优弧
如图,△ABC内接于⊙O,AB=8,AC=6,D是AB边上的一点,P是优弧