题目内容
13.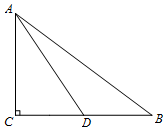 如图,在Rt△ABC中,∠C=90°,点D是BC边的中点,CD=2,tanB=$\frac{3}{4}$.
如图,在Rt△ABC中,∠C=90°,点D是BC边的中点,CD=2,tanB=$\frac{3}{4}$.(1)求AD和AB的长;
(2)求sin∠BAD的值.
分析 (1)由中点定义求BC=4,根据tanB=$\frac{3}{4}$得:AC=3,由勾股定理得:AB=5,AD=$\sqrt{13}$;
(2)作高线DE,证明△DEB∽△ACB,求DE的长,再利用三角函数定义求结果.
解答 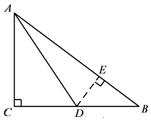 解:(1)∵D是BC的中点,CD=2,
解:(1)∵D是BC的中点,CD=2,
∴BD=DC=2,BC=4,
在Rt△ACB中,由 tanB=$\frac{AC}{CB}=\frac{3}{4}$,
∴$\frac{AC}{4}=\frac{3}{4}$,
∴AC=3,
由勾股定理得:AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5;
(2)过点D作DE⊥AB于E,
∴∠C=∠DEB=90°,
又∠B=∠B,
∴△DEB∽△ACB,
∴$\frac{DE}{AC}=\frac{DB}{AB}$,
∴$\frac{DE}{3}=\frac{2}{5}$,
∴$DE=\frac{6}{5}$,
∴sin∠BAD=$\frac{DE}{AD}$=$\frac{\frac{6}{5}}{\sqrt{13}}$=$\frac{6\sqrt{13}}{65}$.
点评 本题考查了解直角三角形,熟练掌握直角三角形的边角关系是解题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
8.已知点A(1,a)与点B(3,b)都在反比例函数y=-$\frac{12}{x}$的图象上,则a与b之间的关系是( )
| A. | a>b | B. | a<b | C. | a≥b | D. | a=b |
18.直角三角形的两直角边长分别为3cm、4cm以直角顶点为圆心,2.4cm长为半径的圆与斜边的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 无法确定 |
3.下列各式计算正确的是( )
| A. | (a5)2=a7 | B. | 2x-2=$\frac{1}{2{x}^{2}}$ | C. | 4a3•2a2=8a6 | D. | a8÷a2=a6 |
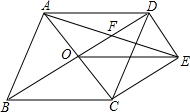 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE.
如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE. 在平面直角坐标系中,A,B,C三点的坐标分别为(-5,4),(-3,0),(0,2).
在平面直角坐标系中,A,B,C三点的坐标分别为(-5,4),(-3,0),(0,2).