题目内容
14.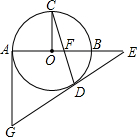 如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE,使∠CDE=∠DFE,DE交AB的延长线于点E.过点A作⊙O的切线交ED的延长线于点G.
如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE,使∠CDE=∠DFE,DE交AB的延长线于点E.过点A作⊙O的切线交ED的延长线于点G.(1)求证:GE是⊙O的切线;
(2)若OA=2,∠G=50°,求弧$\widehat{AD}$的长;
(3)若OF:OB=1:3,BE=4,求OB的长.
分析 (1)连接OD,如图,先证明∠3=∠1,再证明∠C=∠4,然后利用∠3+∠C=90°得到∠1+∠4=90°,则OD⊥DE,然后根据切线的判定定理即可得到结论;
(2)由切线的性质得∠OAG=90°,则利用四边形内角和可计算出∠AOD=130°,然后根据弧长公式可计算出弧$\widehat{AD}$的长;
(3)设OF=x,则OB=3x,则可表示出BF=2x,再利用∠1=∠2得到ED=EF=2x+4,然后在Rt△ODE中,根据勾股定理得到(3x)2+(2x+4)2=(4+3x)2,再解方程求出x即可得到OB的长.
解答 (1)证明:连接OD,如图,
∵∠1=∠2,
而∠2=∠3,
∴∠3=∠1,
∵OC⊥AB,
∴∠3+∠C=90°,
∴∠1+∠C=90°,
而OC=OD,
∴∠C=∠4,
∴∠1+∠4=90°,即∠ODE=90°,
∴OD⊥DE,
∴GE是⊙O的切线;
(2)解:∵AG为切线,
∴AG⊥AB,
∴∠OAG=90°,
而∠ODG=90°,
∴∠AOD=180°-50°=130°,
∴弧$\widehat{AD}$的长=$\frac{130•π•2}{180}$=$\frac{13}{9}$π;
(3)解:设OF=x,则OB=3x,
∴BF=2x,
∵∠1=∠2,
∴ED=EF=2x+4,
在Rt△ODE中,∵OD2+DE2=OE2,
∴(3x)2+(2x+4)2=(4+3x)2,解得x=2,
∴OB=3x=6.
点评 本题考查了切线的判断与性质:圆的切线垂直于经过切点的半径;经过半径的外端且垂直于这条半径的直线是圆的切线.常见的辅助线有:判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”; 有切线时,常常“遇到切点连圆心得半径”.也考查了弧长公式.

练习册系列答案
相关题目
5.计算:
(1)(π-3.14)0-($\frac{1}{2}$)-2+($\frac{1}{3}$)2012×(-3)2012
(2)(a2)6÷a8+(-2a)2(-$\frac{1}{2}$a2)
(1)(π-3.14)0-($\frac{1}{2}$)-2+($\frac{1}{3}$)2012×(-3)2012
(2)(a2)6÷a8+(-2a)2(-$\frac{1}{2}$a2)
2.下列命题正确的是( )
| A. | 若两弦相等,则它们所对的弧相等 | |
| B. | 若弦长等于半径,则弦所对的劣弧的度数为60° | |
| C. | 若两弧不等,则大弧所对的圆心角较大 | |
| D. | 若两弧的度数相等,则两条弧是等弧 |
3.下列语句属于命题的是( )
| A. | 作直线AB的平行线 | B. | 在线段AB上任取一点C | ||
| C. | 等角的余角相等 | D. | 同位角都相等吗? |
4.若2a=5b,则$\frac{a}{b}$=( )
| A. | $\frac{2}{5}$ | B. | $\frac{5}{2}$ | C. | 2 | D. | 5 |
 已知:如图,AC、BD相交于点O,∠A=∠D,AB=CD.
已知:如图,AC、BD相交于点O,∠A=∠D,AB=CD.