题目内容
6. 已知:如图,AC、BD相交于点O,∠A=∠D,AB=CD.
已知:如图,AC、BD相交于点O,∠A=∠D,AB=CD.(1)求证:△AOB≌△DOC;
(2)AC=BD.
分析 (1)由对顶角相等可得∠AOB=∠DOC,然后利用“角角边”证明即可;
(2)根据全等三角形对应边相等可得AO=DO,BO=CO,然后表示出AC、BD,等量代换即可得证.
解答 证明:(1)由对顶角相等得,∠AOB=∠DOC,
在△AOB和△DOC中,$\left\{\begin{array}{l}{∠A=∠D}\\{∠AOB=∠DOC}\\{AB=CD}\end{array}\right.$,
∴△AOB≌△DOC(AAS);
(2)∵△AOB≌△DOC,
∴AO=DO,BO=CO,
∵AC=AO+CO,
BD=DO+BO,
∴AC=BD.
点评 本题考查了全等三角形的判定与性质,熟练掌握三角形全等的判定方法是解题的关键,要注意对顶角相等的应用.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
1.下列说法中:
①有理数的绝对值一定是正数;
②互为相反数的两个数,必然一个是正数,一个是负数;
③若|a|=|b|,则a与b互为相反数;
④绝对值等于本身的数是0;
⑤任何一个数都有它的相反数.
其中正确的个数有( )
①有理数的绝对值一定是正数;
②互为相反数的两个数,必然一个是正数,一个是负数;
③若|a|=|b|,则a与b互为相反数;
④绝对值等于本身的数是0;
⑤任何一个数都有它的相反数.
其中正确的个数有( )
| A. | 0 个 | B. | 1 个 | C. | 2 个 | D. | 3 个 |
15. 如图,已知等边△ABC外有一点P,P落在∠BAC内,设P到BC、CA、AB的距离分别为h1,h2,h3,满足h2+h3-h1=6,那么等边△ABC的面积为( )
如图,已知等边△ABC外有一点P,P落在∠BAC内,设P到BC、CA、AB的距离分别为h1,h2,h3,满足h2+h3-h1=6,那么等边△ABC的面积为( )
 如图,已知等边△ABC外有一点P,P落在∠BAC内,设P到BC、CA、AB的距离分别为h1,h2,h3,满足h2+h3-h1=6,那么等边△ABC的面积为( )
如图,已知等边△ABC外有一点P,P落在∠BAC内,设P到BC、CA、AB的距离分别为h1,h2,h3,满足h2+h3-h1=6,那么等边△ABC的面积为( )| A. | 4$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 9$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
16. 如图,在半径为2cm,圆心角为90°的扇形OAB内,以OB为直径作半圆交弦AB于点C,则图中阴影部分的面积是( )
如图,在半径为2cm,圆心角为90°的扇形OAB内,以OB为直径作半圆交弦AB于点C,则图中阴影部分的面积是( )
 如图,在半径为2cm,圆心角为90°的扇形OAB内,以OB为直径作半圆交弦AB于点C,则图中阴影部分的面积是( )
如图,在半径为2cm,圆心角为90°的扇形OAB内,以OB为直径作半圆交弦AB于点C,则图中阴影部分的面积是( )| A. | π-1 | B. | π-2 | C. | $\frac{1}{2}π-1$ | D. | $\frac{1}{2}π-2$ |

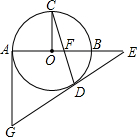 如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE,使∠CDE=∠DFE,DE交AB的延长线于点E.过点A作⊙O的切线交ED的延长线于点G.
如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE,使∠CDE=∠DFE,DE交AB的延长线于点E.过点A作⊙O的切线交ED的延长线于点G.