题目内容
 如图,已知△ABC的外角∠CBD和∠BCE的平分线BF,CF相交于点F,试问点F在∠A的平分线上吗?
如图,已知△ABC的外角∠CBD和∠BCE的平分线BF,CF相交于点F,试问点F在∠A的平分线上吗?考点:角平分线的性质
专题:
分析:过点F分别作FM⊥AB,FN⊥AC,FG⊥BC,垂足分别为M、N、G,根据角平分线的性质可得FM=FN,则可知F在∠A的平分线上.
解答: 解:如图,过点F分别作FM⊥AB,FN⊥AC,FG⊥BC,垂足分别为M、N、G,
解:如图,过点F分别作FM⊥AB,FN⊥AC,FG⊥BC,垂足分别为M、N、G,
∵BF、CF分别平分∠CBD和∠BCE,
∴FM=FG=FN,
∴F在∠A的平分线上.
 解:如图,过点F分别作FM⊥AB,FN⊥AC,FG⊥BC,垂足分别为M、N、G,
解:如图,过点F分别作FM⊥AB,FN⊥AC,FG⊥BC,垂足分别为M、N、G,∵BF、CF分别平分∠CBD和∠BCE,
∴FM=FG=FN,
∴F在∠A的平分线上.
点评:本题主要考查角平分线的判定和性质,掌握角平分线上的点到角两边的距离相等、到角两边距离相等的点在角的平分线上是解题的关键.

练习册系列答案
相关题目
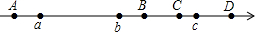 如图,有数数a、b、c在数轴上表示的点,如果|a|>|c|>|b|,那么数轴上的原点0可能是( )
如图,有数数a、b、c在数轴上表示的点,如果|a|>|c|>|b|,那么数轴上的原点0可能是( )| A、在A的位置 |
| B、在B的位置 |
| C、在C的位置 |
| D、在D的位置 |
 如图,小亮用手盖住的点的坐标有可能是( )
如图,小亮用手盖住的点的坐标有可能是( )| A、(-3,-4) |
| B、(-4,3) |
| C、(4,3) |
| D、(3,-4) |
 如图,直线AB、CD相交于点O,∠BOD与∠BOE互为余角,∠BOE=18°,则∠AOC=
如图,直线AB、CD相交于点O,∠BOD与∠BOE互为余角,∠BOE=18°,则∠AOC= 如图,△ABC中,DE垂直平分AC交AB于点E,∠A=30°,∠B=70°,则∠BCE=
如图,△ABC中,DE垂直平分AC交AB于点E,∠A=30°,∠B=70°,则∠BCE= 已知一个几何体的主视图和俯视图如图,请根据已知视图想象几何体的可能形状,并按照你的想象补画出两种不同的左视图.
已知一个几何体的主视图和俯视图如图,请根据已知视图想象几何体的可能形状,并按照你的想象补画出两种不同的左视图. 如图,已知BD是∠ABC的角平分线,DE⊥AB于E点,AB=6cm,BC=4cm,S△ABC=10cm2,则DE=
如图,已知BD是∠ABC的角平分线,DE⊥AB于E点,AB=6cm,BC=4cm,S△ABC=10cm2,则DE=