题目内容
 如图,△ABC中,DE垂直平分AC交AB于点E,∠A=30°,∠B=70°,则∠BCE=
如图,△ABC中,DE垂直平分AC交AB于点E,∠A=30°,∠B=70°,则∠BCE=考点:线段垂直平分线的性质
专题:
分析:根据△ABC中DE垂直平分AC,可求出AE=CE,再根据等腰三角形的性质求出∠ACE=∠A=30°,再由∠A=30°,∠B=70°,根据三角形内角和定理可求∠ACB的度数,即可解答.
解答:解:∵DE垂直平分AC,∠A=30°,
∴AE=CE,
∴∠ACE=∠A=30°,
∵∠A=30°,∠B=70°,
∴∠ACB=80°,
∴∠BCE=∠ACB-∠ACE=80°-30°=50°.
故答案为:50°.
∴AE=CE,
∴∠ACE=∠A=30°,
∵∠A=30°,∠B=70°,
∴∠ACB=80°,
∴∠BCE=∠ACB-∠ACE=80°-30°=50°.
故答案为:50°.
点评:本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等边对等角的性质,熟记性质是解题的关键.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
x=-2是下列( )方程的解.
| A、5x+7=7-2x | ||
| B、6x-8=8x-4 | ||
| C、3x-2=4+x | ||
D、
|
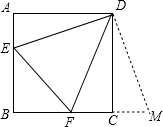 正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM. 如图,已知△ABC的外角∠CBD和∠BCE的平分线BF,CF相交于点F,试问点F在∠A的平分线上吗?
如图,已知△ABC的外角∠CBD和∠BCE的平分线BF,CF相交于点F,试问点F在∠A的平分线上吗? 如图,△ABC中,∠ACB=90°,CD是高,若∠A=30°,BD=1,则AD=
如图,△ABC中,∠ACB=90°,CD是高,若∠A=30°,BD=1,则AD=