题目内容
18.如果m、n是两个不相等的实数,且满足m2-2m=1,n2-2n=1,那么代数式2m2+4n2-4n+2015=2029.分析 由m、n满足m2-2m=1、n2-2n=1,即可得出m2=1+2m,n2=1+2n、m、n为方程x2-2x-1=0的两个实数根,再根据根与系数的关系即可得出m+n=2,将m2=1+2m,n2=1+2n、m+n=2代入2m2+4n2-4n+2015中即可求出结论.
解答 解:∵m、n满足m2-2m=1、n2-2n=1,
∴m、n为方程x2-2x-1=0的两个实数根,m2=1+2m,n2=1+2n,
∴m+n=2,mn=-1.
∴2m2+4n2-4n+2015=2(1+2m)+4(1+2n)-4n+2015=2+4m+4+8n-4n+2015=4m+4n+2021=2029.
故答案为:2029.
点评 本题考查了根与系数的关系以及一元二次方程的解,根据m、n满足m2-2m=1、n2-2n=1找出m+n=2,将m2=1+2m,n2=1+2n、m+n=2是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
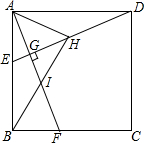 如图,正方形ABCD中,E,F分别为AB边,BC边上,且DE⊥AF于点G,H为线段DG上一点,连接AH,BH,BH交AF于点l,若∠GAH=45°,GI=1.正方形ABCD边长为4,则△AHD面积为$\sqrt{7}$-1.
如图,正方形ABCD中,E,F分别为AB边,BC边上,且DE⊥AF于点G,H为线段DG上一点,连接AH,BH,BH交AF于点l,若∠GAH=45°,GI=1.正方形ABCD边长为4,则△AHD面积为$\sqrt{7}$-1. 如图,在平面直角坐标系xOy中,点A(4,3),点B(6,0),边AB上有一点P(m,1),点M,N分别在边OB、OA上,联结MN,MN∥AB,联结PM、PN、AM.
如图,在平面直角坐标系xOy中,点A(4,3),点B(6,0),边AB上有一点P(m,1),点M,N分别在边OB、OA上,联结MN,MN∥AB,联结PM、PN、AM.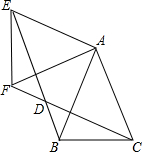 如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D
如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D