题目内容
在平面直角坐标系中，已知点A（-
，0），B（
，0），点C在坐标轴上，且AC+BC=6，则满足条件的点C有（ ）个．
| 5 |
| 5 |
| A、1 | B、2 | C、3 | D、4 |
考点：勾股定理,坐标与图形性质
专题：
分析：需要分类讨论：①当点C位于x轴上时，根据线段间的和差关系即可求得点C的坐标；②当点C位于y轴上时，根据勾股定理求点C的坐标．
解答：
解：如图，①当点C位于y轴上时，设C（0，b）．
则
+
=6，解得，b=2或
b=-2，
此时C（0，2），或C（0，-2）．
如图，②当点C位于x轴上时，设C（a，0）．
则|-
-a|+|a-
|=6，即2a=6或-2a=6，
解得a=3或a=-3，
此时C（-3，0），或C（3，0）．
综上所述，点C的坐标是：（0，2），（0，-2），（-3，0），（3，0）．
故选D．
解：如图，①当点C位于y轴上时，设C（0，b）．则
(
|
| (-5)2+b2 |
b=-2，
此时C（0，2），或C（0，-2）．
如图，②当点C位于x轴上时，设C（a，0）．
则|-
| 5 |
| 5 |
解得a=3或a=-3，
此时C（-3，0），或C（3，0）．
综上所述，点C的坐标是：（0，2），（0，-2），（-3，0），（3，0）．
故选D．
点评：本题考查了勾股定理、坐标与图形的性质．解题时，要分类讨论，以防漏解．另外，当点C在y轴上时，也可以根据两点间的距离公式来求点C的坐标．
练习册系列答案
相关题目
满足下列条件的△ABC，不是直角三角形的是（ ）
| A、b2=a2-c2 |
| B、a：b：c=3：4：5 |
| C、∠C=∠A-∠B |
| D、∠A：∠B：∠C=3：4：5 |
小红想知道我校旗杆的高度，她发现旗杆顶端的绳子长13米，绳子拉直后，下端离旗杆底5米，则旗杆的高度是（ ）| A、10米 | B、11米 |
| C、12米 | D、14米 |
若a的相反数是5，则a的倒数是（ ）
A、-
| ||
| B、-5 | ||
C、
| ||
| D、5 |
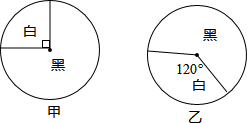游戏组织者用如图所示的甲，乙两个转盘设计了一个游戏，规定：游戏参与者交1元钱可以分别转动甲，乙两个转盘各一次，若转盘停止时两指针的指向为下表中的组合：