题目内容
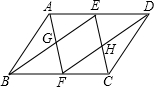 如图,在?ABCD中,点E和点F分别是AD、BC上的点,且AE=CF,AF与BE交于点G,DF与CE交于点H,求证:四边形EGFH是平行四边形.
如图,在?ABCD中,点E和点F分别是AD、BC上的点,且AE=CF,AF与BE交于点G,DF与CE交于点H,求证:四边形EGFH是平行四边形.考点:平行四边形的判定与性质
专题:证明题
分析:可分别证明四边形AFCE是平行四边形,四边形BFDE是平行四边形,从而得出GF∥EH,GE∥FH,即可证明四边形EGFH是平行四边形.
解答:证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵AE=CF,DE=BF
∴四边形AECF是平行四边形.
∴GF∥EH.
∵ED∥BF且ED=BF.
∴四边形BFDE是平行四边形.
∴GE∥FH.
∴四边形EGFH是平行四边形.
∴AD∥BC,AD=BC.
∵AE=CF,DE=BF
∴四边形AECF是平行四边形.
∴GF∥EH.
∵ED∥BF且ED=BF.
∴四边形BFDE是平行四边形.
∴GE∥FH.
∴四边形EGFH是平行四边形.
点评:本题考查了平行四边形的判定和性质,证明四边形AECF和BFDE是平行四边形是关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 已知B是线段AC延长线一点.D是AB中点,E是BC中点,DE=6,求AC的长度.
已知B是线段AC延长线一点.D是AB中点,E是BC中点,DE=6,求AC的长度.
 如图,点O在直线AB上,∠BOD=90°,∠COE=90°,图中互补的角有
如图,点O在直线AB上,∠BOD=90°,∠COE=90°,图中互补的角有