题目内容
阅读下列材料:
方程
-
=
-
的解为x=1
方程
-
=
-
的解为x=2
方程
-
=
-
的解为x=3
…
(1)请你观察上述方程与解的特征,写出能反映上述方程一般规律的方程,并才想这个方程的解.
(2)利用(1)中所得的结论,写出一个解为x=2009的分式方程.
方程
| 1 |
| x+1 |
| 1 |
| x |
| 1 |
| x-2 |
| 1 |
| x-3 |
方程
| 1 |
| x |
| 1 |
| x-1 |
| 1 |
| x-3 |
| 1 |
| x-4 |
方程
| 1 |
| x-1 |
| 1 |
| x-2 |
| 1 |
| x-4 |
| 1 |
| x-5 |
…
(1)请你观察上述方程与解的特征,写出能反映上述方程一般规律的方程,并才想这个方程的解.
(2)利用(1)中所得的结论,写出一个解为x=2009的分式方程.
考点:分式方程的解
专题:规律型
分析:(1)归纳总结得到一般性规律,写出第n个方程,表示出方程的解即可;
(2)利用得出的规律确定出分式方程即可.
(2)利用得出的规律确定出分式方程即可.
解答:解:(1)方程
-
=
-
的解为x=n;
(2)根据得出的规律得:解为x=2009的分式方程为
-
=
-
.
| 1 |
| x-(n-2) |
| 1 |
| x-(n-1) |
| 1 |
| x-(n+1) |
| 1 |
| x-(n+2) |
(2)根据得出的规律得:解为x=2009的分式方程为
| 1 |
| x-2007 |
| 1 |
| x-2008 |
| 1 |
| x-2010 |
| 1 |
| x-2011 |
点评:此题考查了分式方程的解,弄清题中的规律是解本题的关键.

练习册系列答案
相关题目
下列计算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
计算:
×
+3
的结果为( )
| 2 |
| 8 |
| -81 |
| A、-1 | ||
| B、1 | ||
C、4-33
| ||
| D、7 |
 如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.画出位似中心点O,并直接写出△ABC与△A′B′C′的位似比.
如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.画出位似中心点O,并直接写出△ABC与△A′B′C′的位似比.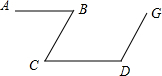 如图,∠ABC=∠BCD,∠ABC+∠CDG=180°,试问:BC与GD平行吗?若平行,请说明理由.
如图,∠ABC=∠BCD,∠ABC+∠CDG=180°,试问:BC与GD平行吗?若平行,请说明理由.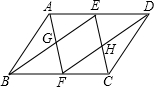 如图,在?ABCD中,点E和点F分别是AD、BC上的点,且AE=CF,AF与BE交于点G,DF与CE交于点H,求证:四边形EGFH是平行四边形.
如图,在?ABCD中,点E和点F分别是AD、BC上的点,且AE=CF,AF与BE交于点G,DF与CE交于点H,求证:四边形EGFH是平行四边形.