题目内容
如果某个二次函数的图象经过平移后能与y=3x2的图象重合,那么这个二次函数的解析式可以是 .(只要写出一个).
考点:二次函数图象与几何变换
专题:开放型
分析:先设原抛物线的解析式为y=a(x-h)2+k,再根据经过平移后能与抛物线y=3x2重合可知a=3,然后根据平移的性质写出解析式,答案不唯一.
解答:解:先设原抛物线的解析式为y=a(x+h)2+k,
∵经过平移后能与抛物线y=3x2重合,
∴a=3,
∴这个二次函数的解析式可以是y=3(x+2)2+3.
故答案为:y=3(x+2)2+3.
∵经过平移后能与抛物线y=3x2重合,
∴a=3,
∴这个二次函数的解析式可以是y=3(x+2)2+3.
故答案为:y=3(x+2)2+3.
点评:本题考查的是二次函数的图象与几何变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
相关题目
估算
+2的值( )
| 24 |
| A、在5和6之间 |
| B、在8和9之间 |
| C、在7和8之间 |
| D、在6和7之间 |
抛物线y=2x2,y=-2x2,y=
x2共有的性质是( )
| 1 |
| 2 |
| A、开口向下 |
| B、对称轴是y轴 |
| C、都有最低点 |
| D、y的值随x的增大而减小 |
下列运算中,不正确的是( )
| A、(-a3)2=a9 |
| B、a3+a3=2a3 |
| C、a2•a3=a5 |
| D、2a3÷a2=2a |
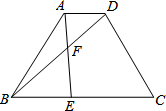 如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC.
如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC.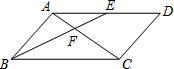 已知:如图,?ABCD中,E是AD中点,BE交AC于点F,设
已知:如图,?ABCD中,E是AD中点,BE交AC于点F,设