题目内容
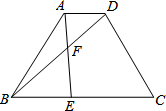 如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC.
如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC.(1)求证:△ABE∽△BCD;
(2)求tan∠DBC的值;
(3)求线段BF的长.
考点:相似三角形的判定与性质,等腰梯形的性质
专题:
分析:(1)根据等腰梯形可得到∠ABE=∠C,结合条件可证得结论;
(2)过D作DG⊥BC,则可求得BG、CG,在Rt△DCG中可求得DG,在Rt△BGD中由正切函数的定义可求得tan∠DBC;
(3)由(2)可求得BD,结合(1)中的相似可求得BE,再利用平行线分线段成比例得到
=
,代入可求得BF.
(2)过D作DG⊥BC,则可求得BG、CG,在Rt△DCG中可求得DG,在Rt△BGD中由正切函数的定义可求得tan∠DBC;
(3)由(2)可求得BD,结合(1)中的相似可求得BE,再利用平行线分线段成比例得到
| AD |
| BE |
| DF |
| BF |
解答:(1)证明:∵四边形ABCD为等腰梯形,
∴∠ABE=∠C,且∠BAE=∠DBC,
∴△ABE∽△BCD;
(2)解:过D作DG⊥BC于点G,
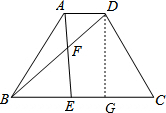
∵AD=1,BC=3,
∴CG=
(BC-AD)=1,BG=2,
又∵在Rt△DGC中,CD=2,CG=1,
∴DG=
,
在Rt△BDG中,tan∠DBC=
=
;
(3)解:由(2)在Rt△BGD中,由勾股定理可求得BD=
,
由(1)△ABE∽△BCD可得
=
,即=
=
,解得BE=
,
又∵AD∥BC,
∴
=
,且DF=BD-BF,
∴
=
,
解得BF=
.
∴∠ABE=∠C,且∠BAE=∠DBC,
∴△ABE∽△BCD;
(2)解:过D作DG⊥BC于点G,

∵AD=1,BC=3,
∴CG=
| 1 |
| 2 |
又∵在Rt△DGC中,CD=2,CG=1,
∴DG=
| 3 |
在Rt△BDG中,tan∠DBC=
| DG |
| BG |
| ||
| 2 |
(3)解:由(2)在Rt△BGD中,由勾股定理可求得BD=
| 7 |
由(1)△ABE∽△BCD可得
| AB |
| BC |
| BE |
| CD |
| BE |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
又∵AD∥BC,
∴
| AD |
| BE |
| DF |
| BF |
∴
| 1 | ||
|
| ||
| BF |
解得BF=
4
| ||
| 7 |
点评:本题主要考查相似三角形的判定和性质及三角函数的定义,在(2)中构造直角三角形,求得DG是解题的关键,在(3)中求得BE、BD的长是解题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 如图,轮船C在观测站A的北偏东60°方向,在观测站B的北偏西45°方向,则从轮船C看A、B两站的视角∠ACB=( )
如图,轮船C在观测站A的北偏东60°方向,在观测站B的北偏西45°方向,则从轮船C看A、B两站的视角∠ACB=( )| A、105° | B、100° |
| C、120° | D、110° |
抛物线y=-x2+x-1与坐标轴(含x轴、y轴)的公共点的个数是( )
| A、0 | B、1 | C、2 | D、3 |
在Rt△ABC中,∠C=90°,如果∠A=α,AB=c,那么BC等于( )
| A、c•sinα |
| B、c•cosα |
| C、c•tanα |
| D、c•cotα |
 如图,张岩同学在湖岸边的一座大楼DN中,观测湖对岸的一座古塔AB,已知这座大楼与古塔的水平距离是20
如图,张岩同学在湖岸边的一座大楼DN中,观测湖对岸的一座古塔AB,已知这座大楼与古塔的水平距离是20
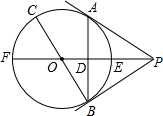 如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F,过点A作PO的垂线AB,垂足为D,交⊙O于点B,BO的延长线交⊙O于点C.
如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F,过点A作PO的垂线AB,垂足为D,交⊙O于点B,BO的延长线交⊙O于点C.