��Ŀ����
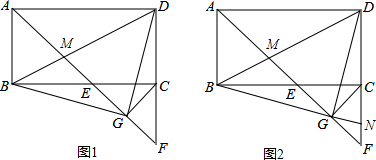
17�� ��ͼ����ƽ��ֱ������ϵ�У�������y=a��x-1��2-4a��a��0����x����A��B���㣬��A�ڵ�B����ߣ��䶥��Ϊ��C��һ���������µ������߾���A��B��D���㣬�䶥��D��x���Ϸ�������������Ϊ3������AC��AD��CD��
��ͼ����ƽ��ֱ������ϵ�У�������y=a��x-1��2-4a��a��0����x����A��B���㣬��A�ڵ�B����ߣ��䶥��Ϊ��C��һ���������µ������߾���A��B��D���㣬�䶥��D��x���Ϸ�������������Ϊ3������AC��AD��CD����1��ֱ��д��A��B��������ꣻ
��2����A��B��D���������������Ӧ�ĺ�������ʽ��
��3������ACDΪ����������ʱ����a��ֵ��
��4�����߶�AC�Ƶ�A��ת90�㣬����C�Ķ�Ӧ��ǡ�����ڣ�2���е��������ϣ�ֱ��д��a��ֵ��
���� ��1�����ݵ���ص㣬��y=0��������̵Ľ⣬���ɣ�
��2�����������߽���ʽȷ������C��D������ͶԳ��᷽�̣�������������ʽ���ɣ�
��3����ACDΪ����������ʱ��������������㣺����CDΪ��ʱ����C��D����x��Գƣ�����������⣬����ACΪ��ʱ����AD=CD������������⣬����ADΪ��ʱ����AC=CD������������⼴�ɣ�
��4���ȱ�ʾ��ֱ��AC�Ľ���ʽΪy=-2ax-2a���Ӷ����ֱ��l�������ߵĽ���M��$\frac{9a-2}{3a}$��$\frac{6a-1}{3{a}^{2}}$����Ȼ���ʾ��AM��AC�������̼��ɣ�
��� �⣺��1����y=0��
��a��x-1��2-4a=0��
��a��0��
�ࣨx-1��2-4=0
��x1=-1��x2=3��
��A��-1��0����B��3��0����
��2����y=a��x-1��2-4a��
�������ߵĶ���C��1��-4a�����Գ���Ϊx=1��
��D��1��3����
�辭��A��B��D����������߽���ʽΪy=m��x-1��2+3��
��m=-$\frac{3}{4}$��
�ྭ��A��B��D����������߽���ʽΪy=-$\frac{3}{4}$��x-1��2+3=-$\frac{3}{4}$x2+$\frac{3}{2}$x+$\frac{9}{4}$��
��3������ACDΪ����������ʱ��������������㣬
����CDΪ��ʱ����C��D����X��Գƣ�
��C��1��-3����
��-4a=-3��
��a=$\frac{3}{4}$��
����ACΪ��ʱ����AD=CD��
���ݹ��ɶ����ã�AD=$\sqrt{A{E}^{2}+D{E}^{2}}$=$\sqrt{13}$��
��CD=2-��-4a��=3+4a=$\sqrt{13}$��
��a=$\frac{\sqrt{13}-3}{4}$��
����ADΪ��ʱ����AC=CD��
���ݹ��ɶ����ã�AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=2$\sqrt{4{a}^{2}+1}$��
��CD=3-��-4a��=2$\sqrt{4{a}^{2}+1}$��
��a=-$\frac{5}{24}$��0���ᣩ��
��4���ɣ�1��֪��A��-1��0����C��1��4a����AC=2$\sqrt{4{a}^{2}+1}$��
��ֱ��AC�Ľ���ʽΪy=-2ax-2a��
���߶�AC�Ƶ�A��ת90��õ���ֱ��Ϊl��
��l��AC�ҹ���A��
��ֱ��l����ʽΪy=$\frac{1}{2a}$x+$\frac{1}{2a}$��
��������y=-$\frac{3}{4}$x2+$\frac{3}{2}$x+$\frac{9}{4}$��
��3ax2+��2-6a��x+2-9a=0��
��x1=1���ᣩ��x2=$\frac{9a-2}{3a}$��
��ֱ��l�������ߵĽ���M��$\frac{9a-2}{3a}$��$\frac{6a-1}{3{a}^{2}}$����
��AM=|6a-1|��$\frac{\sqrt{4{a}^{2}+1}}{3{a}^{2}}$��
��AM=AC��
��2$\sqrt{4{a}^{2}+1}$=|6a-1|��$\frac{\sqrt{4{a}^{2}+1}}{3{a}^{2}}$��
��6a2=|6a-1|
��6a-1��0ʱ��6a2=6a-1��
��a=$\frac{3��\sqrt{3}}{6}$��
��6a-1��0ʱ��6a2=1-6a��
��a=-3��$\sqrt{3}$���ᣩ��
����a1=$\frac{3+\sqrt{3}}{6}$��a2=$\frac{3-\sqrt{3}}{6}$��
���� �����Ƕ��κ����ۺ��⣬��Ҫ������������������ķ������÷��̵�˼�������⣬���õ����ɶ������Ȿ��Ĺؼ����÷��̵�˼�룮

| A�� | 33��104 | B�� | 3.3��104 | C�� | 3.3��105 | D�� | 0.33��106 |
| A�� | 616 | B�� | 68 | C�� | 68+1 | D�� | 68-1 |
| A�� | ������1�����Ǻ��� | B�� | ������1�����ǰ��� | ||
| C�� | ������2�����Ǻ��� | D�� | ������2�����ǰ��� |
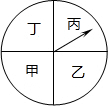 ��ͼ����һ������������ת��ת�̵ȷֳɼס��ҡ��������ĸ�����������ָ��̶����䣬ת�����ת��һ�Σ����ָ��ָ�ڵȷ����ϣ���ô����ת����ֱ��ָ��ָ��ij������������Ϊֹ������ָ��ָ�ڱ������ڵĸ����ǣ�������
��ͼ����һ������������ת��ת�̵ȷֳɼס��ҡ��������ĸ�����������ָ��̶����䣬ת�����ת��һ�Σ����ָ��ָ�ڵȷ����ϣ���ô����ת����ֱ��ָ��ָ��ij������������Ϊֹ������ָ��ָ�ڱ������ڵĸ����ǣ�������| A�� | 1 | B�� | $\frac{1}{2}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{1}{4}$ |