题目内容
13．下列命题中，真命题的是（ ）| A． | 两条对角线相等的四边形是矩形 | |
| B． | 两条对角线互相平分的四边形是平行四边形 | |
| C． | 两条对角线互相垂直且相等的四边形是正方形 | |
| D． | 两条对角线互相垂直的四边形是菱形 |
分析 根据矩形的判定方法对A进行判断；根据平行四边形的判定方法对B进行判断；根据正方形的判定方法对C进行判断；根据菱形的判定方法对D进行判断．
解答 解：A、两条对角线相等平行四边形是矩形，所以A选项错误；
B、两条对角线互相平分的四边形是平行四边形，所以B选项正确；
C、两条对角线互相垂直平分且相等的四边形是正方形，所以C选项错误；
D、两条对角线互相垂直的平行四边形是菱形，所以D选项错误．
故选B．
点评 本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．
练习册系列答案
相关题目
如图，△ABC内接于⊙O，∠C=45°，AB=2，则⊙O的半径为$\sqrt{2}$．
如图，矩形ABCD顶点在y=$\frac{1}{x}$上，且S矩形ABCD=2$\sqrt{5}$，则A的坐标xA=$\frac{\sqrt{5}+1}{2}$，yA=$\frac{\sqrt{5}-1}{2}$．
18．
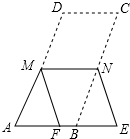如图，在?ABCD中，∠A=70°，将?ABCD折叠，使点D、C分别落在点F、E处（点F、E都在AB所在的直线上），折痕为MN，则∠AMF等于（ ）
如图，在?ABCD中，∠A=70°，将?ABCD折叠，使点D、C分别落在点F、E处（点F、E都在AB所在的直线上），折痕为MN，则∠AMF等于（ ）| A． | 70° | B． | 40° | C． | 30° | D． | 20° |
2．计算$\sqrt{8}$×$\sqrt{\frac{1}{2}}$+（$\sqrt{5}$）0的结果为（ ）
| A． | 2+$\sqrt{2}$ | B． | $\sqrt{2}$+1 | C． | 3 | D． | 5 |
1．
如图，用火柴棍摆出一系列三角形图案，按这种方法摆下去，第五个图案需要火柴棍总数为（ ）
如图，用火柴棍摆出一系列三角形图案，按这种方法摆下去，第五个图案需要火柴棍总数为（ ）| A． | 31根 | B． | 42根 | C． | 45根 | D． | 51根 |