题目内容
1. 如图,△ABC内接于⊙O,∠C=45°,AB=2,则⊙O的半径为$\sqrt{2}$.
如图,△ABC内接于⊙O,∠C=45°,AB=2,则⊙O的半径为$\sqrt{2}$.
分析 首先连接OA,OB,由∠C=45°,易得△AOB是等腰直角三角形,继而求得答案.
解答  解:连接OA,OB,
解:连接OA,OB,
∵∠C=45°,
∴∠AOB=2∠C=90°,
∵OA=OB,
∴△OAB是等腰直角三角形,
∴OA=AB•cos45°=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 此题考查了圆周角定理以及等腰直角三角形性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
9.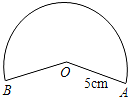 小明用图中所示的扇形纸片作一个圆锥的侧面,小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个的圆锥的高是( )
小明用图中所示的扇形纸片作一个圆锥的侧面,小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个的圆锥的高是( )
 小明用图中所示的扇形纸片作一个圆锥的侧面,小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个的圆锥的高是( )
小明用图中所示的扇形纸片作一个圆锥的侧面,小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个的圆锥的高是( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 2cm |
16.下列说法中正确的是( )
| A. | 四边相等的四边形是菱形 | |
| B. | 一组对边相等,另一组对边平行的四边形是菱形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线互相平分的四边形是菱形 |
13.下列命题中,真命题的是( )
| A. | 两条对角线相等的四边形是矩形 | |
| B. | 两条对角线互相平分的四边形是平行四边形 | |
| C. | 两条对角线互相垂直且相等的四边形是正方形 | |
| D. | 两条对角线互相垂直的四边形是菱形 |
10.下面调查中,适合采用普查的是( )
| A. | 调查全国中学生心理健康现状 | |
| B. | 调查你所在的班级同学的身高情况 | |
| C. | 调查我市食品合格情况 | |
| D. | 调查苏州电视台《新闻夜班车》的收视率 |
10.已知反比例函数y=$\frac{10}{x}$,当2.5<x<5时,y的取值范围是( )
| A. | 2<y<4 | B. | 2.5<x<5 | C. | 5<y<10 | D. | y>10 |
 如图,在6×6的正方形网格中,△ABC的顶点在格点上,请仅用无刻度的直尺分别在图①、图②中画出△ABC的AB边上的高.
如图,在6×6的正方形网格中,△ABC的顶点在格点上,请仅用无刻度的直尺分别在图①、图②中画出△ABC的AB边上的高.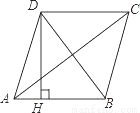
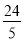 B.
B.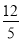 C.5 D.4
C.5 D.4 如图中所示是一圆锥形的零件经过轴的剖面,它的腰长等于圆锥的母线长,底边长等于圆锥底面的直径,按图中表明的尺寸求这个零件的母线长为36.
如图中所示是一圆锥形的零件经过轴的剖面,它的腰长等于圆锥的母线长,底边长等于圆锥底面的直径,按图中表明的尺寸求这个零件的母线长为36.