题目内容
6.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.求销售单价为多少元时,每天的销售利润最大?最大利润是多少?分析 根据“利润=(售价-成本)×销售量”列出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;把二次函数解析式转化为顶点式方程,利用二次函数图象的性质进行解答.
解答 解:设每天的销售利润y元,销售单价x元,
y=(x-50)[50+5(100-x)]
=(x-50)(-5x+550)
=-5x2+800x-27500
∴y=-5x2+800x-27500,
=-5(x-80)2+4500
∵a=-5<0,
∴抛物线开口向下,
∵50≤x≤100,对称轴是直线x=80,
∴当x=80时,y最大值=4500.
点评 此题题考查二次函数的实际应用,为数学建模题,借助二次函数解决实际问题,解决本题的关键是二次函数图象的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列命题中,真命题的是( )
| A. | 两条对角线相等的四边形是矩形 | |
| B. | 两条对角线互相平分的四边形是平行四边形 | |
| C. | 两条对角线互相垂直且相等的四边形是正方形 | |
| D. | 两条对角线互相垂直的四边形是菱形 |

 ,过点M作 MG⊥EF交线段BC的延长线于点G.
,过点M作 MG⊥EF交线段BC的延长线于点G. 如图,在6×6的正方形网格中,△ABC的顶点在格点上,请仅用无刻度的直尺分别在图①、图②中画出△ABC的AB边上的高.
如图,在6×6的正方形网格中,△ABC的顶点在格点上,请仅用无刻度的直尺分别在图①、图②中画出△ABC的AB边上的高.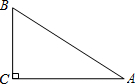 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=1,
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=1,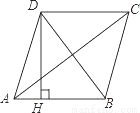
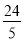 B.
B.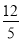 C.5 D.4
C.5 D.4