题目内容
在Rt△ABC中,∠A=90°,∠B=30°, AC=1,点O在BC上,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,则⊙O的半径为 ;∠MND的度数为 。

 ;300。
;300。
【考点】切线的性质,含30度角直角三角形的性质,正方形的判定和性质,平行的判定和性质,相似三角形的判定和性质,圆周角定理。
【分析】如图,连接O E,
在Rt△ABC中,∠A=900,∠B=30 °, AC=1,
°, AC=1,

∴AB= 。
。
∵⊙O与AB、AC相切,∴OD⊥AB,OE⊥AC。

又∵在Rt△ABC中,∠A=90°,∠B=30°,∴∠C=60°。
∵OD∥CA,∴∠DOM=60°。
∴∠MND= ∠DOM=30°。
∠DOM=30°。

练习册系列答案
相关题目
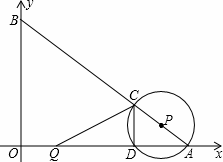
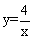 图象上,点B在反比例函数
图象上,点B在反比例函数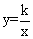 (k≠0)的图象上,CB∥x轴,BD∥AO,若CA=
(k≠0)的图象上,CB∥x轴,BD∥AO,若CA=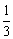 CB,则双曲线
CB,则双曲线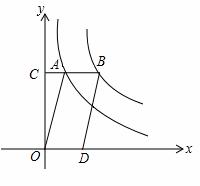


 自行车和摩托车行驶过程的函数解析式(不要求写出自变量的取值范围);
自行车和摩托车行驶过程的函数解析式(不要求写出自变量的取值范围); 或不等式(不要化简,也不要求解):①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面.
或不等式(不要化简,也不要求解):①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面. ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC
ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC 、PF⊥BD,垂足分别为E、F。
、PF⊥BD,垂足分别为E、F。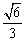 PE,PE=
PE,PE= ,EO=1,求∠EPF的度数;
,EO=1,求∠EPF的度数; -4,求BC的长。
-4,求BC的长。
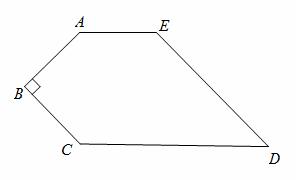
 BD;
BD; EB;
EB; 求阴影部分的面积。
求阴影部分的面积。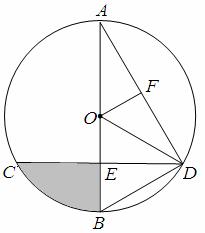


 A;
A; ,并求出使
,并求出使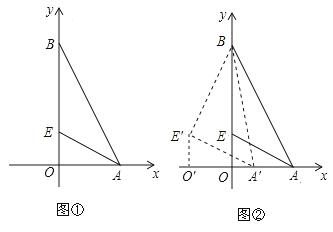

 t为何值时,DQ=2AD?
t为何值时,DQ=2AD?