题目内容
如图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象(分别为正比例函数和一次函数).两地间的距离是80千米.请你根据图象回答或解决下面的问题:


(1)谁出发的较早?早多长时间?谁到达乙地较早?早到多长时间?
(2)两人在途中行驶的速度分别是多少?
(3)请你分别求出表示 自行车和摩托车行驶过程的函数解析式(不要求写出自变量的取值范围);
自行车和摩托车行驶过程的函数解析式(不要求写出自变量的取值范围);
(4)指出在什么时间段内两车均行驶在途中(不包括端点);在这一时间段内,请你分别按下列条件列出关于时间x的方程 或不等式(不要化简,也不要求解):①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面.
或不等式(不要化简,也不要求解):①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面.
(1)自行车出发早3个小时,摩托车到达乙地早3个小时
(2)10千米/时,40千米/时
(3)自行车:y=10x,摩托车:y=40x-120
(4)在3<x<5时间段内两车均都行驶在途中, 自行车在摩托车前面:10x>40x-120
自行车在摩托车前面:10x>40x-120 ,相遇:10x=40x-120,自行车在摩托车后:10x<40x-120
,相遇:10x=40x-120,自行车在摩托车后:10x<40x-120
【解析】

(3)设表示自行车行驶过程的函数解析式为y=kx.
x=8时,y=80
因此k=10
∴表示自行车行驶过 程的函数式是y=10x.
程的函数式是y=10x.
设表示摩托车行驶过程的函数解析式是y=ax+b
由题意可知:
 ,解得
,解得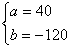

∴表示摩托车行驶过程的函数解析式为y=40x-120.

考点:本题考查的是一次函数的应用
点评:本题是利用一次 函数的有关知识解答实际应用题,借助函数图象表达题目中的信息,读懂图象是关键.
函数的有关知识解答实际应用题,借助函数图象表达题目中的信息,读懂图象是关键.

练习册系列答案
相关题目
 其各位上的四个数字的平方和等于个位、千位数字乘积的2倍与十位、百位数字乘积的2倍之和,且个位与十位数字相同
其各位上的四个数字的平方和等于个位、千位数字乘积的2倍与十位、百位数字乘积的2倍之和,且个位与十位数字相同 的图象如下列四个图之一所示,根据
的图象如下列四个图之一所示,根据 图象分析,a的值等于【 】
图象分析,a的值等于【 】
 x+b(a>0)、二次函数y=ax2+bx和反比例函数y=
x+b(a>0)、二次函数y=ax2+bx和反比例函数y=
 (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( )

 方程
方程 有实数根x1,x2,且x1≠x2,有下列结论:
有实数根x1,x2,且x1≠x2,有下列结论: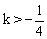 ;
; 的图象与x轴交点的坐标
的图象与x轴交点的坐标 (1,0)和(2,0)。
(1,0)和(2,0)。 写有数
写有数 字﹣2,﹣1,1的卡片,它们的背面完全相
字﹣2,﹣1,1的卡片,它们的背面完全相 同,将这
同,将这 三张卡片北背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值,不放回卡片洗匀,再从余下的两张卡片中随机抽取
三张卡片北背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值,不放回卡片洗匀,再从余下的两张卡片中随机抽取 一张,以其正面的数字作为y的值,两次结果记为(x,y)。
一张,以其正面的数字作为y的值,两次结果记为(x,y)。 图或列表法表示(x,y)所有可能出现的结果;
图或列表法表示(x,y)所有可能出现的结果; 无意义的(x,y)
无意义的(x,y) 长方形ACBD和长方形AEFB(如图2)。
长方形ACBD和长方形AEFB(如图2)。

 中的要求把它补成长方形,那么符合要求的长方形可以画出 个,利用图3把它画出来。
中的要求把它补成长方形,那么符合要求的长方形可以画出 个,利用图3把它画出来。
 到与AB相切于点D的位置,则⊙O自转了【 】
到与AB相切于点D的位置,则⊙O自转了【 】