题目内容
8.先化简,再求值($\frac{3x}{x-1}$-$\frac{x}{x+1}$)•$\frac{{x}^{2}-1}{x}$,其中x=-5.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{3x(x+1)-x(x-1)}{(x-1)(x+1)}$•$\frac{(x+1)(x-1)}{x}$
=$\frac{3{x}^{2}+3x-{x}^{2}+x}{(x-1)(x+1)}$•$\frac{(x+1)(x-1)}{x}$
=$\frac{2{x(x+2)}^{\;}}{(x-1)(x+1)}$•$\frac{(x+1)(x-1)}{x}$
=x(x+2),
当x=-5时,原式=-5×(-5+2)=15.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
16.“十一”黄金周,山西乔家大院迎来了全国各地的游客,小渝就是数万游客中的一个;他在游览过程中,对传统建筑非常感兴趣.并发现窗户的每个窗格上都贴有剪纸.如图,其中“O”代表的就是剪纸.请问第6个图中剪纸的个数为( )


| A. | 20 | B. | 23 | C. | 25 | D. | 30 |
20.某厂今年3月的产值为72万元,5月下降到50万元,这两个月平均每月降低的百分率是多少?若设平均每月降低的百分率为x,则列出方程是( )
| A. | 50(1+x)=72 | B. | 50(1+x)+50(1+x)2=72 | C. | 50(1-x)2=72 | D. | 72(1-x)2=50 |
17. 如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A是100°第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A是100°第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
 如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A是100°第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A是100°第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
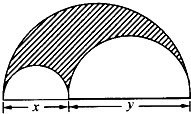 如图,一块半圆形钢板,从中挖去直径分别为x、y的两个半圆:
如图,一块半圆形钢板,从中挖去直径分别为x、y的两个半圆: 如图为一次函数y=kx+b的图象,则一次函数y=bx+k的图象大致是( )
如图为一次函数y=kx+b的图象,则一次函数y=bx+k的图象大致是( )

