题目内容
4.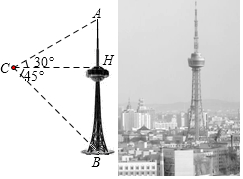 吉林省广播电视塔(简称“吉塔”)是我省目前最高的人工建筑,也是俯瞰长春市美景的最佳去处.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度.已知如图将无人机置于距离“吉塔”水平距离138米的点C处,则从无人机上观测塔尖的仰角恰为30°,观测塔基座中心点的俯角恰为45°.求“吉塔”的高度.(注:$\sqrt{3}$≈1.73,结果保留整数)
吉林省广播电视塔(简称“吉塔”)是我省目前最高的人工建筑,也是俯瞰长春市美景的最佳去处.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度.已知如图将无人机置于距离“吉塔”水平距离138米的点C处,则从无人机上观测塔尖的仰角恰为30°,观测塔基座中心点的俯角恰为45°.求“吉塔”的高度.(注:$\sqrt{3}$≈1.73,结果保留整数)
分析 根据在Rt△ACH中,tan∠ACH=$\frac{AH}{CH}$,求出AH的值,再根据△BCH是等腰直角三角形,求出BH=CH=138米,最后根据AB=AH+BH,即可求出答案.
解答  解:如图,根据题意,有∠ACH=30°,∠HCB=45°,CH=138米,
解:如图,根据题意,有∠ACH=30°,∠HCB=45°,CH=138米,
在Rt△ACH中,∵tan∠ACH=$\frac{AH}{CH}$,
∴tan30°=$\frac{AH}{138}$,
∴AH=138×$\frac{\sqrt{3}}{3}$=46$\sqrt{3}$≈79.58,
在Rt△BCD中,∵∠DCB=45°,CD=138,
∴BH=CH=138米,
∴AB=AH+BH≈79.58+138≈218.
答:“吉塔”的高度约为218米.
点评 此题考查了解直角三角形的应用-仰角俯角问题,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
14.我校为了解七年级男同学参加课外体育运动的情况,随机调查了50名七年级男同学,其中,参加篮球运动的有14人,乒乓球运动的有11人,足球运动的有13人,其余参加羽毛球运动.则参加羽毛球运动的频率是( )
| A. | 0.28 | B. | 0.28 | C. | 0.26 | D. | 0.24 |
12.当a=1,b=-2时,代数式2a2-ab的值是( )
| A. | -4 | B. | 0 | C. | 4 | D. | 7 |
9.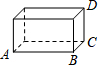 如图:长方体的长AB=4厘米、宽BC=2厘米、高CD=3厘米.一只蚂蚁想从A点沿表面爬到D点,则最短距离是( )
如图:长方体的长AB=4厘米、宽BC=2厘米、高CD=3厘米.一只蚂蚁想从A点沿表面爬到D点,则最短距离是( )
 如图:长方体的长AB=4厘米、宽BC=2厘米、高CD=3厘米.一只蚂蚁想从A点沿表面爬到D点,则最短距离是( )
如图:长方体的长AB=4厘米、宽BC=2厘米、高CD=3厘米.一只蚂蚁想从A点沿表面爬到D点,则最短距离是( )| A. | 3$\sqrt{5}$ | B. | $\sqrt{41}$ | C. | $\sqrt{29}$ | D. | 5 |
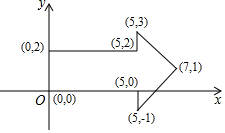 如图,箭头图案是将坐标分别为(0,0),(0,2),(5,2),(5,3),(7,1),(5,-1),(5,0),(0,0)的点用线段依次连接而成的,现把图中的格点分别如下变换:
如图,箭头图案是将坐标分别为(0,0),(0,2),(5,2),(5,3),(7,1),(5,-1),(5,0),(0,0)的点用线段依次连接而成的,现把图中的格点分别如下变换: