题目内容
10．写出一个抛物线开口向下，与y轴交于（0，2）点的函数表达式y=-x2+x+2（答案不唯一）．分析 首先根据开口向下得到二次项系数小于0，然后根据与y轴的交点坐标的纵坐标为2得到c值即可得到函数的解析式．
解答 解：∵开口向下，
∴y=ax2+bx+c中a＜0，
∵与y轴交于（0，2）点，
∴c=2，
∴抛物线的解析式可以为：y=-x2+x+2（答案不唯一）．
故答案为：y=-x2+x+2（答案不唯一）．
点评 本题考查了二次函数的性质，属于开放型题目，答案不唯一，所写抛物线的解析式满足a＜0，c=2即可．
练习册系列答案
名校课堂系列答案
相关题目
20．一个直角三角形的斜边和一条直角边的长分别为17、15，则另一条直角边的长是（ ）
| A． | 8 | B． | 16 | C． | 10 | D． | 14 |
如图，点A、B、C、D、E在圆上，弦的延长线与弦的延长线相交于点，AB是圆的直径，D是BC的中点．求证：AB=AC．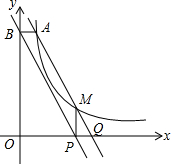
如图，点A（3，2）和点M（m，n）都在反比例函数y=$\frac{k}{x}$（x＞0）的图象上．