题目内容
 在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东 60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),那么,由此可知,B、C两地相距
在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东 60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),那么,由此可知,B、C两地相距考点:等腰三角形的判定与性质,方向角
专题:
分析:先求出∠BAC,再根据三角形的内角和定理求出∠C,从而得到∠BAC=∠C,然后根据等角对等边可得BC=AB.
解答:解:∵B在A的正东方,C在A地的北偏东 60°方向,
∴∠BAC=90°-60°=30°,
∵C在B地的北偏东30°方向,
∴∠ABC=90°+30°=120°,
∴∠C=180°-∠BAC-∠ABC=180°-30°-120°=30°,
∴∠BAC=∠C,
∴BC=AB=200m.
故答案为:200.
∴∠BAC=90°-60°=30°,
∵C在B地的北偏东30°方向,
∴∠ABC=90°+30°=120°,
∴∠C=180°-∠BAC-∠ABC=180°-30°-120°=30°,
∴∠BAC=∠C,
∴BC=AB=200m.
故答案为:200.
点评:本题考查了等腰三角形的判定与性质,方向角的定义,根据角的度数求出∠BAC=∠C是解题的关键,也是本题的难点.

练习册系列答案
相关题目
下列方程中是一元一次方程的是( )
A、
| ||
| B、x2-2x-1=0 | ||
| C、3x-y=4 | ||
D、
|
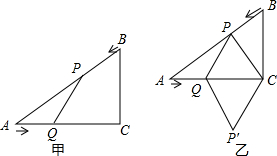 如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题: 如图,直线y=kx+b经过A(-1,1)和B(-3,0)两点,则关于x的不等式组0<kx+b<-x的解集为
如图,直线y=kx+b经过A(-1,1)和B(-3,0)两点,则关于x的不等式组0<kx+b<-x的解集为 如图,为农村一古老的捣碎器,已知支撑柱AB的高为0.4m,踏板DE长为1.2m,支撑点A到踏脚D的距离为0.6m,现在从捣头点E着地的位置开始,让踏脚D着地,则捣头点E上升
如图,为农村一古老的捣碎器,已知支撑柱AB的高为0.4m,踏板DE长为1.2m,支撑点A到踏脚D的距离为0.6m,现在从捣头点E着地的位置开始,让踏脚D着地,则捣头点E上升 如图,已知点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=
如图,已知点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=