题目内容
17.已知点A(2a-b,5+a),B(2b-1,-a+b).(1)若点A,B关于x轴对称,求a,b的值;
(2)若A,B关于y轴对称,求(4a+b)2016的值.
分析 (1)根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”列方程组求解即可;
(2)根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数;”列方程组求出a、b的值,然后代入代数式进行计算即可得解.
解答 解:(1)∵点A,B关于x轴对称,
∴$\left\{\begin{array}{l}{2a-b=2b-1}\\{5+a=-(-a+b)}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-8}\\{b=-5}\end{array}\right.$;
(2)∵A,B关于y轴对称,
∴$\left\{\begin{array}{l}{2a-b=-(2b-1)}\\{5+a=-a+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$,
所以,(4a+b)2016=[4×(-1)+3]2016=1.
点评 本题考查了关于原点对称的点的坐标,关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;(3)关于原点对称的点,横坐标与纵坐标都互为相反数.

练习册系列答案
相关题目
5. 如图,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠ACD=$\frac{4}{5}$,BC=10,则AB的长为( )
如图,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠ACD=$\frac{4}{5}$,BC=10,则AB的长为( )
 如图,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠ACD=$\frac{4}{5}$,BC=10,则AB的长为( )
如图,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠ACD=$\frac{4}{5}$,BC=10,则AB的长为( )| A. | 5 | B. | 6 | C. | 8 | D. | 5$\sqrt{3}$ |
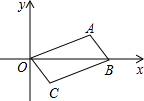 如图,已知?OABC,其中O、A、B、C的坐标分别为O(0,0),A(3,a),B(4,0),C(b,-1).
如图,已知?OABC,其中O、A、B、C的坐标分别为O(0,0),A(3,a),B(4,0),C(b,-1).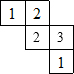 由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其正方形中的数字表示该位置上的小正方体的个数,画出该几何体的主视图.
由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其正方形中的数字表示该位置上的小正方体的个数,画出该几何体的主视图.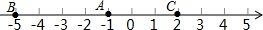 在数轴上有三个点A,B,C,回答下列问题:
在数轴上有三个点A,B,C,回答下列问题:
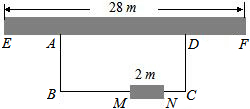 如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).用砌60米长的墙的材料.
如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).用砌60米长的墙的材料.