题目内容
9. 如图,∠1和∠3互余,∠2和∠3的余角互补,若∠4=105°,则∠3等于75°.
如图,∠1和∠3互余,∠2和∠3的余角互补,若∠4=105°,则∠3等于75°.
分析 根据∠1和∠3互余,∠2和∠3的余角互补可得出∠1+∠3=90°,∠2+(90°-∠3)=180°,再由四边形的内角和等于360°可知∠1+∠2+∠3+∠4=360°,三式联立即可得出∠3的度数.
解答 解:∵∠1和∠3互余,∠2和∠3的余角互补,
∴∠1+∠3=90°①,∠2+(90°-∠3)=180°②,
∵四边形的内角和等于360°,
∴∠1+∠2+∠3+∠4=360°③,
把①代入③得,∠2+∠4=270°,
∵∠4=105°,
∴∠2=270°-105°=165°,
把∠2=165°代入②得,∠3=165°-90°=75°.
故答案为:75°.
点评 本题考查的是角的计算,熟知四边形的内角和等于360°是解答此题的关键.

练习册系列答案
相关题目
19.下列命题中正确的是( )
| A. | 对角线相等的四边形一定是平行四边形 | |
| B. | 一组对边平行,一组对角相等的四边形是平行四边形 | |
| C. | 四条边相等的四边形是正方形 | |
| D. | 菱形的对角线互相平分且相等 |
 在Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠ACD=3∠BCD,E是AB的中点,
在Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠ACD=3∠BCD,E是AB的中点, 中国象棋中的马从点(2,3)走到点(5,2)至少需要几步?从点(2,3)走到(3,3)至少需要几步,试写出各步走到的点的坐标.
中国象棋中的马从点(2,3)走到点(5,2)至少需要几步?从点(2,3)走到(3,3)至少需要几步,试写出各步走到的点的坐标.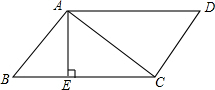 如图,在?ABCD中,AE⊥BC,垂足为E,且E为BC中点,若?ABCD的周长为20cm,△ABC的周长比?ABCD的周长少6cm,求?ABCD各边的长.
如图,在?ABCD中,AE⊥BC,垂足为E,且E为BC中点,若?ABCD的周长为20cm,△ABC的周长比?ABCD的周长少6cm,求?ABCD各边的长.