题目内容
4.已知函数y=kx+b的图象经过点(4,0),且与x轴y轴构成三角形面积为6,求此函数解析式.分析 先根据面积求出三角形在y轴上边的长度,再分正半轴和负半轴两种情况讨论求解.
解答 解:根据题意,设与y轴交点坐标为(0,b)
则$\frac{1}{2}$×4×|b|=6,
解得|b|=3,∴b=±3,
①当b=3时,与y轴交点为(0,3)
把(4,0)(0,3)代入y=kx+b得,
$\left\{\begin{array}{l}{4k+b=0}\\{b=3}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=3}\end{array}\right.$,
∴函数解析式为:y=-$\frac{3}{4}$x+3;
②当b=-3时,与y轴的交点为(0,-3),
把(4,0)(0,-3)代入y=kx+b得,
$\left\{\begin{array}{l}{4k+b=0}\\{b=-3}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=-3}\end{array}\right.$,
∴函数解析式为:y=$\frac{3}{4}$x-3;
因此这个一次函数的解析式是y=-$\frac{3}{4}$x+3或y=$\frac{3}{4}$x-3.
点评 本题主要考查待定系数法求一次函数解析式,利用三角形的面积求得与y轴的交点坐标是解题的关键,注意此题需要分情况讨论.

练习册系列答案
相关题目
12.法国游泳中心“水立方”的外层膜的展开面积约为260000平方米,将260000用科学记数法表示应为( )
| A. | 2.6×104 | B. | 2.6×105 | C. | 0.26×105 | D. | 0.26×106 |

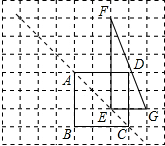 如图,方格纸中每个小正方形的边长均为1,正方形ABCD和△EFG的顶点都在小正方形的顶点上.
如图,方格纸中每个小正方形的边长均为1,正方形ABCD和△EFG的顶点都在小正方形的顶点上. 如图,∠1和∠3互余,∠2和∠3的余角互补,若∠4=105°,则∠3等于75°.
如图,∠1和∠3互余,∠2和∠3的余角互补,若∠4=105°,则∠3等于75°. 如图,已知AC、BD相交于点O,∠B=∠C=90°,且AB=4,OB=OD=3,CD=2,求AC的长.
如图,已知AC、BD相交于点O,∠B=∠C=90°,且AB=4,OB=OD=3,CD=2,求AC的长.