题目内容
3. 如图,D、E是△ABC的边AB和AC中点,延长DE到F,使EF=DE,连结CF.四边形BCFD是平行四边形吗?为什么?
如图,D、E是△ABC的边AB和AC中点,延长DE到F,使EF=DE,连结CF.四边形BCFD是平行四边形吗?为什么?
分析 先证明DE是△ABC的中位线,由三角形中位线定理得出DE∥BC,DE=$\frac{1}{2}$BC,再由已知条件得出DF=BC,即可得出结论.
解答 解:四边形BCFD是平行四边形;理由如下:
∵D、E是△ABC的边AB和AC中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=$\frac{1}{2}$BC,
∵EF=DE,
∴DF=BC,
∴四边形BCFD是平行四边形.
点评 本题考查了三角形中位线定理、平行四边形的判定;熟练掌握三角形中位线定理,并能进行推理论证是解决问题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
13.某厂的生产流水线每小时可生产100件产品,生产前没有产品积压,生产3小时后安排2人装箱,若3小时装产品150件,未装箱的产品数量(y)是时间(t)的函数,这个函数的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
11. 如图,在△ABC中,AB=AC,D是BC延长线上的一点,∠A=40°,则∠ACD等于( )
如图,在△ABC中,AB=AC,D是BC延长线上的一点,∠A=40°,则∠ACD等于( )
 如图,在△ABC中,AB=AC,D是BC延长线上的一点,∠A=40°,则∠ACD等于( )
如图,在△ABC中,AB=AC,D是BC延长线上的一点,∠A=40°,则∠ACD等于( )| A. | 80° | B. | 100° | C. | 110° | D. | 120° |
13.在数轴上与-3的距离等于4的点表示的数是( )
| A. | 1 | B. | -7 | C. | -1或7 | D. | 1或-7 |
 如图,△ABC中,AB=AC,∠BAC与∠BCA的平分线AD、CD交于点D,若∠BAC=80°,则∠ADC=115°.
如图,△ABC中,AB=AC,∠BAC与∠BCA的平分线AD、CD交于点D,若∠BAC=80°,则∠ADC=115°.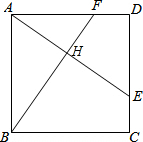 如图,正方形ABCD中,点E、F分别为边CD、AD上的点,CE=DF,AE、BF交于点H
如图,正方形ABCD中,点E、F分别为边CD、AD上的点,CE=DF,AE、BF交于点H 如图,要建一个面积为130m2的仓库,仓库的一边靠墙(墙长16米),并在与墙平行的一边开一道1米宽的门.现有能围成32米长的木板,求仓库的长和宽.
如图,要建一个面积为130m2的仓库,仓库的一边靠墙(墙长16米),并在与墙平行的一边开一道1米宽的门.现有能围成32米长的木板,求仓库的长和宽.