题目内容
9.休息日小明和妈妈从家里出发一同去外婆家,他们走了1小时后爸爸发现带给外婆的礼品忘在家里,便立刻带上礼品以每小时6千米的速度去追,如果小明和妈妈每小时行2千米,从家里到外婆家需要1小时45分钟,问爸爸能在小明和妈妈到外婆家之前追上他们吗?分析 等量关系为:爸爸所走的路程=小明和妈妈所走的路程.
解答 解:设爸爸追上小明需要x小时.
由题意得:6x=2+2x,
解这个方程得:x=$\frac{1}{2}$.
则弟弟行走了1+$\frac{1}{2}$=1小时30分<1小时45分,未到外婆家,即:爸爸能够追上.
答:爸爸能在小明和妈妈到外婆家之前追上他们.
点评 本题考查了一元一次方程的应用.难点是得到弟弟和妈妈所用的时间,关键是找到相应的等量关系.

练习册系列答案
相关题目
4.某商家独家销售具有地方特色的某种商品,每件进价为40元,经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:
(1)试销过程发现,一周销量y(万件)与销售单价x(元/件)之间关系可以近似地看作一次函数,直接写出y与x的函数关系式:y=-10x+1000(x≥50)
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润不低于8000元?
(3)在雅安地震发生时,商家已将商品一周的销售利润全部寄往灾区,已知商家购进该商品的货款不超过10000元,请你分析该商家当时最大捐款数额是多少元?
| 销售单价x(元/件) | … | 55 | 60 | 70 | 75 | … |
| 一周的销售量y(件) | … | 450 | 400 | 300 | 250 | … |
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润不低于8000元?
(3)在雅安地震发生时,商家已将商品一周的销售利润全部寄往灾区,已知商家购进该商品的货款不超过10000元,请你分析该商家当时最大捐款数额是多少元?
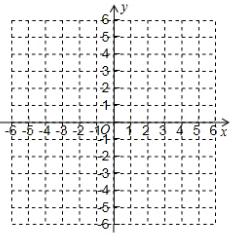 如图,在平面直角坐标系中,已知菱形ABCD顶点的坐标分别为A(1,-1),B(5,a),C(1,3),D(b,c),在图中画出菱形ABCD,并写出a,b,c的值.
如图,在平面直角坐标系中,已知菱形ABCD顶点的坐标分别为A(1,-1),B(5,a),C(1,3),D(b,c),在图中画出菱形ABCD,并写出a,b,c的值.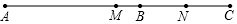 如图,点B在线段AC上,点M、N分别是AC、BC的中点.
如图,点B在线段AC上,点M、N分别是AC、BC的中点. 如图,已知线段AB
如图,已知线段AB